题目内容
在△ABC中，AB=AC，过点A的直线与其外接圆交于点P，交BC延长线于点D．求证：AP•AD=AB•AC
考点：与圆有关的比例线段
专题：立体几何
分析：首先利用等腰三角形和四点共圆的性质得到△APC∽△ACD的充分条件，然后根据相似三角形的性质得到结论．
解答：
证明：在△ABC中，AB=AC，所以∠ABC=∠ACB，
因为：∠ABC+∠APC=180°
∠ACB+∠ACD=180°
所以：∠ACD=∠APC
∠CAP为公共角
所以△APC∽△ACD，
所以
=
所以AC2=AP•AD
由AB=AC，
所以AP•AD=AB•AC．
因为：∠ABC+∠APC=180°
∠ACB+∠ACD=180°
所以：∠ACD=∠APC
∠CAP为公共角
所以△APC∽△ACD，
所以
| AP |
| AC |
| AC |
| AD |
所以AC2=AP•AD
由AB=AC，
所以AP•AD=AB•AC．
点评：本题考查的知识点：四点共圆的性质，三角形相似的判定和性质．属于基础题型．
练习册系列答案
相关题目
如图，在三棱柱ABC-A1B1C1中，M为A1C1的中点，面AB1M∥面BC1N，CA∩面BC1N=N．求证：N为AC的中点．
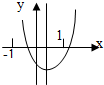已知二次函数f（x）=ax2+bx+c（a≠0）的图象如图所示，设M=|a+b+c|-|a-b+c|+|2a+b|-|2a-b，则（ ）| A、M＞0 | B、M≥0 |
| C、M＜0 | D、M=0 |
如图，在△ABC中，∠C=90°，点E是AC上一点，ED⊥AB，cosA=