题目内容
已知抛物线y2=8x的准线与圆（x-1）2+y2=25交于A、B两点，则|AB|= ．
考点：抛物线的简单性质,直线与圆的位置关系
专题：圆锥曲线的定义、性质与方程
分析：求出抛物线的准线方程，利用圆心到直线的距离与半径与半弦长的关系，即可求出弦长．
解答：
解：抛物线y2=8x的准线方程为：x=-2，
圆（x-1）2+y2=25的圆心坐标（1，0），半径为5，
圆心到直线的距离为：3，
抛物线y2=8x的准线与圆（x-1）2+y2=25交于A、B两点，则|AB|=2
=8．
故答案为：8．
圆（x-1）2+y2=25的圆心坐标（1，0），半径为5，
圆心到直线的距离为：3，
抛物线y2=8x的准线与圆（x-1）2+y2=25交于A、B两点，则|AB|=2
| 52-32 |
故答案为：8．
点评：本题考查抛物线方程的应用，抛物线的几何性质，直线与圆的位置关系，基本知识的考查．
练习册系列答案
相关题目
已知{an}是等比数列，若a6＞0，则a6＜a9是a6＜a7的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
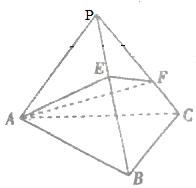如图，在三棱锥P-ABC中，三个侧面都是顶角为20°的等腰三角形，侧棱长均为a，E、F分别是PB、PC上的点，则△AEF周长的最小值为（ ）