题目内容
如图，在△ABC中，∠C=90°，点E是AC上一点，ED⊥AB，cosA=| 2 |
| 5 |
| 5 |
| 4 |
| 3 |
| 5 |
考点：相似三角形的性质
专题：立体几何
分析：由题意可设AD=2
x，AE=5x，由勾股定理可得DE=
x，由cosA=
=
可得x的方程，解x可得DE
| 5 |
| 5 |
| AC |
| AB |
| 2 |
| 5 |
| 5 |
解答：
解：由题意结合cosA=
可设AD=2
x，AE=5x，
由勾股定理可得DE=
=
x，
又tan∠BED=
，∴BD=
DE=
x，
∵cosA=
=
=
，解得x=
∴DE=
x=3
| 2 |
| 5 |
| 5 |
| 5 |
由勾股定理可得DE=
(5x)2-(2
|
| 5 |
又tan∠BED=
| 4 |
| 3 |
| 4 |
| 3 |
4
| ||
| 3 |
∵cosA=
| AC |
| AB |
5x+
| ||||||
2
|
| 2 |
| 5 |
| 5 |
| 3 | ||
|
∴DE=
| 5 |
点评：本题考查相似三角形，涉及三角函数和勾股定理的应用，属基础题．
练习册系列答案
相关题目
函数y=
+
的值域是（ ）
| ||
| cosx |
| ||
| sinx |
| A、{0，2} |
| B、{-2，2} |
| C、{0，-2} |
| D、{-2，0，2} |
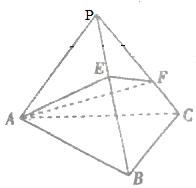如图，在三棱锥P-ABC中，三个侧面都是顶角为20°的等腰三角形，侧棱长均为a，E、F分别是PB、PC上的点，则△AEF周长的最小值为（ ）