题目内容
已知不等式组
表示的平面区域恰好被圆C:(x-3)2+(y-3)2=r2所覆盖,则实数k的值是( )
|
| A、3 | B、4 | C、5 | D、6 |
考点:简单线性规划
专题:计算题,作图题,不等式的解法及应用
分析:由题意作出其平面区域,则可知,(0,-6)关于(3,3)的对称点(6,12)在x-y+k=0上,从而解出k.
解答:
解:由题意作出其平面区域,

由平面区域恰好被圆C:(x-3)2+(y-3)2=r2所覆盖可知,
平面区域所构成的三角形的三个顶点都在圆上,
又∵三角形为直角三角形,
∴(0,-6)关于(3,3)的对称点(6,12)在x-y+k=0上,解得k=6,
故选D.

由平面区域恰好被圆C:(x-3)2+(y-3)2=r2所覆盖可知,
平面区域所构成的三角形的三个顶点都在圆上,
又∵三角形为直角三角形,
∴(0,-6)关于(3,3)的对称点(6,12)在x-y+k=0上,解得k=6,
故选D.
点评:本题考查了简单线性规划,作图要细致认真,属于中档题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
已知定点A、B,且|AB|=2,动点P满足|PA|-|PB|=1,则点P的轨迹为( )
| A、双曲线 | B、双曲线一支 |
| C、两条射线 | D、一条射线 |
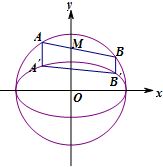 如图,设AB、A′B′分别是圆O:x2+y2=4和椭圆C:
如图,设AB、A′B′分别是圆O:x2+y2=4和椭圆C: