题目内容
已知定点A、B,且|AB|=2,动点P满足|PA|-|PB|=1,则点P的轨迹为( )
| A、双曲线 | B、双曲线一支 |
| C、两条射线 | D、一条射线 |
考点:双曲线的定义
专题:圆锥曲线的定义、性质与方程
分析:首先利用动点P满足|PA|-|PB|=1<|AB|=2,进一步求出点P是以A、B为焦点,以x轴,y轴为对称轴的双曲线的右支.最后确定方程的结果.
解答:
解:动点P满足|PA|-|PB|=1<|AB|=2,
所以:点P是以A、B为焦点,以x轴,y轴为对称轴的双曲线的右支.
所以设双曲线的方程为:
-
=1(a>0,b>0)
根据|PA|-|PB|=1=2a
解得:a=
|AB|=2=2c
解得:c=1
由于:a2+b2=c2
解得:b2=
所以解得双曲线方程为:4x2-
=1
故选:B
所以:点P是以A、B为焦点,以x轴,y轴为对称轴的双曲线的右支.
所以设双曲线的方程为:
| x2 |
| a2 |
| y2 |
| b2 |
根据|PA|-|PB|=1=2a
解得:a=
| 1 |
| 2 |
|AB|=2=2c
解得:c=1
由于:a2+b2=c2
解得:b2=
| 3 |
| 4 |
所以解得双曲线方程为:4x2-
| 4y2 |
| 3 |
故选:B
点评:本题考查的知识要点:双曲线方程的定义,双曲线的方程.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
函数f(x)=alnx-x+
的定义域内无极值,则实数a的取值范围( )
| a+3 |
| x |
| A、[3,-2] |
| B、[-2,6] |
| C、[-3,6] |
| D、[-3,+2] |
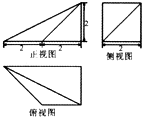
某几何体的三视图如图所示,则这个几何体的体积为( )

A、
| ||
B、
| ||
| C、8 | ||
| D、4 |
计算
(1-cosx)dx=( )
| ∫ |
-
|
| A、π+2 | B、π-2 | C、π | D、-2 |
抛物线 x2=y的准线方程是( )
| A、4x+1=0 |
| B、4y+1=0 |
| C、2x+1=0 |
| D、2y+1=0 |