题目内容
已知曲线C:
-y2=1(an>0,n∈N*)的一个焦点为F(
,0).
(1)求an,
(2)令bn=
,Tn=b1+b2+…+bn,求Tn.
| x2 | ||
|
| n2+1 |
(1)求an,
(2)令bn=
| 1 |
| anan+1 |
考点:双曲线的简单性质,数列的求和
专题:等差数列与等比数列
分析:(1)由于曲线C:
-y2=1(an>0,n∈N*)的一个焦点为F(
,0).可得
+1=n2+1,解出即可.
(2)由于bn=
=
=
-
,利用“裂项求和”即可得出.
| x2 | ||
|
| n2+1 |
| a | 2 n |
(2)由于bn=
| 1 |
| anan+1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
解答:
解:(1)∵曲线C:
-y2=1(an>0,n∈N*)的一个焦点为F(
,0).
∴
+1=n2+1,
∴an=n.
(2)∵bn=
=
=
-
,
∴Tn=b1+b2+…+bn
=(1-
)+(
-
)+…+(
-
)
=1-
=
.
| x2 | ||
|
| n2+1 |
∴
| a | 2 n |
∴an=n.
(2)∵bn=
| 1 |
| anan+1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Tn=b1+b2+…+bn
=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
=
| n |
| n+1 |
点评:本题考查了双曲线的性质、“裂项求和”的方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
函数f(x)=alnx-x+
的定义域内无极值,则实数a的取值范围( )
| a+3 |
| x |
| A、[3,-2] |
| B、[-2,6] |
| C、[-3,6] |
| D、[-3,+2] |
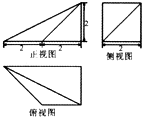
某几何体的三视图如图所示,则这个几何体的体积为( )

A、
| ||
B、
| ||
| C、8 | ||
| D、4 |
抛物线 x2=y的准线方程是( )
| A、4x+1=0 |
| B、4y+1=0 |
| C、2x+1=0 |
| D、2y+1=0 |
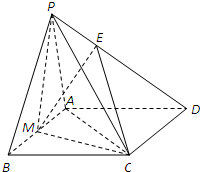 在四棱锥P-ABCD中,PA=PB.底面ABCD是菱形,且∠ABC=60°.E在棱PD上,满足PE=2DE,M是AB的中点.
在四棱锥P-ABCD中,PA=PB.底面ABCD是菱形,且∠ABC=60°.E在棱PD上,满足PE=2DE,M是AB的中点.