题目内容
设a∈R,函数f(x)=lnx-ax.
(1)若a=2,求曲线y=f(x)在x=1处的切线方程;
(2)若a<
,试判断函数f(x)在x∈(1,e2)的零点个数,并说明你的理由;
(3)若f(x)有两个相异零点x1,x2,求证:x1•x2>e2.
(1)若a=2,求曲线y=f(x)在x=1处的切线方程;
(2)若a<
| 2 |
| e2 |
(3)若f(x)有两个相异零点x1,x2,求证:x1•x2>e2.
考点:利用导数研究函数的极值,利用导数研究曲线上某点切线方程
专题:压轴题,转化思想,导数的综合应用
分析:先求导.
对第(1)问,将a的值代入,得切线的斜率,接着求切点,利用点斜式得切线方程;
对第(2)问,思路一:先分“a≤0”和“a>0”讨论,当a≤0时,结论易见,当a>0时,由极值点确定再次分类的标准,然后利用函数的单调性、零点定理,根据区间的端点及图象分析零点的个数,思路二:考虑方程f(x)=0,将参数a分离,将零点问题转化为两函数图象交点问题,再利用导数研究函数的单调性,从而由两函数图象的位置关系确定零点个数;
对第(3)问,根据已知,将求证式进行等价转换,最后通过构造函数,利用函数的单调性达到证明的目的.
对第(1)问,将a的值代入,得切线的斜率,接着求切点,利用点斜式得切线方程;
对第(2)问,思路一:先分“a≤0”和“a>0”讨论,当a≤0时,结论易见,当a>0时,由极值点确定再次分类的标准,然后利用函数的单调性、零点定理,根据区间的端点及图象分析零点的个数,思路二:考虑方程f(x)=0,将参数a分离,将零点问题转化为两函数图象交点问题,再利用导数研究函数的单调性,从而由两函数图象的位置关系确定零点个数;
对第(3)问,根据已知,将求证式进行等价转换,最后通过构造函数,利用函数的单调性达到证明的目的.
解答:
解:在区间(0,+∞)上,f′(x)=
-a=
.
(1)当a=2时,切线的斜率k=f′(1)=
=-1,
又f(1)=ln1-2×1=-2,
由点斜式得切线方程为y-(-2)=-(x-1),即x+y+1=0.
(2)方法一:
(i)当a≤0时,f'(x)≥0,则f(x)在(1,e2)上单调递增,
此时f(1)=-a≥0,∴f(x)在x∈(1,e2)没有零点;
(ii)当a>0时,令f'(x)=0,得x=
.
①当0<a≤
即
≥e2时,则
当x∈(1,e2),有f′(x)≥0,从而f(x)在(1,e2)单调递增,
此时f(1)=-a<0,f(e2)=lne2-ae2=2-ae2>0,
∴f(x)在x∈(1,e2)有且只有一个零点.
②当
<a<
即
<
<e2时,则
当x∈(1,
)时,f′(x)>0,f(x)在(1,
)单调递增;
当x∈(
,e2)时,f′(x)<0,f(x)在(
,e2)单调递减.
而f(
)=ln
-1>0,f(1)=-a<0,f(e2)=2-ae2>0,
∴f(x)在x∈(1,e2)有且只有一个零点.
综上,当a≤0时,f(x)在x∈(1,e2)没有零点;
当0<a<
时,函数f(x)有且只有一个零点.
方法二:由f(x)=0,得a=
,
函数f(x)在x∈(1,e2)的零点个数等价于函数y=a的图象与函数y=
的图象的交点个数,
令g(x)=
,则g′(x)=
,
由g'(x)=0,得x=e,
在区间(1,e)上,g'(x)>0,则函数g(x)是增函数,
∴g(1)<g(x)<g(e),即0<g(x)<
;
在区间(e,e2)上,g'(x)<0,则函数g(x)是减函数,
∴g(e2)<g(x)<g(e),即
<g(x)<
.
∵a<
,∴当a≤0时,f(x)在x∈(1,e2)没有零点;
当0<a<
时,函数f(x)有且只有一个零点.
(3)原不等式x1•x2>e2?lnx1+lnx2>2.
不妨设x1>x2>0,∵f(x1)=0,f(x2)=0,∴lnx1-ax1=0,lnx2-ax2=0,
∴lnx1+lnx2=a(x1+x2),lnx1-lnx2=a(x1-x2),
∴a(x1+x2)>2?
>
?ln
>
.
令
=t,则t>1,于是ln
>
?lnt>
.
设函数h(t)=lnt-
(t>1),则h′(t)=
-
=
>0,
故函数h(t)在(1,+∞)上为增函数,∴h(t)>h(1)=0,
即不等式lnt>
成立,故所证不等式x1•x2>e2成立.
| 1 |
| x |
| 1-ax |
| x |
(1)当a=2时,切线的斜率k=f′(1)=
| 1-2×1 |
| 1 |
又f(1)=ln1-2×1=-2,
由点斜式得切线方程为y-(-2)=-(x-1),即x+y+1=0.
(2)方法一:
(i)当a≤0时,f'(x)≥0,则f(x)在(1,e2)上单调递增,
此时f(1)=-a≥0,∴f(x)在x∈(1,e2)没有零点;
(ii)当a>0时,令f'(x)=0,得x=
| 1 |
| a |
①当0<a≤
| 1 |
| e2 |
| 1 |
| a |
当x∈(1,e2),有f′(x)≥0,从而f(x)在(1,e2)单调递增,
此时f(1)=-a<0,f(e2)=lne2-ae2=2-ae2>0,
∴f(x)在x∈(1,e2)有且只有一个零点.
②当
| 1 |
| e2 |
| 2 |
| e2 |
| e2 |
| 2 |
| 1 |
| a |
当x∈(1,
| 1 |
| a |
| 1 |
| a |
当x∈(
| 1 |
| a |
| 1 |
| a |
而f(
| 1 |
| a |
| 1 |
| a |
∴f(x)在x∈(1,e2)有且只有一个零点.
综上,当a≤0时,f(x)在x∈(1,e2)没有零点;
当0<a<
| 2 |
| e2 |
方法二:由f(x)=0,得a=
| lnx |
| x |
函数f(x)在x∈(1,e2)的零点个数等价于函数y=a的图象与函数y=
| lnx |
| x |
令g(x)=
| lnx |
| x |
| 1-lnx |
| x2 |
由g'(x)=0,得x=e,
在区间(1,e)上,g'(x)>0,则函数g(x)是增函数,
∴g(1)<g(x)<g(e),即0<g(x)<
| 1 |
| e |
在区间(e,e2)上,g'(x)<0,则函数g(x)是减函数,
∴g(e2)<g(x)<g(e),即
| 2 |
| e2 |
| 1 |
| e |
∵a<
| 2 |
| e2 |
当0<a<
| 2 |
| e2 |
(3)原不等式x1•x2>e2?lnx1+lnx2>2.
不妨设x1>x2>0,∵f(x1)=0,f(x2)=0,∴lnx1-ax1=0,lnx2-ax2=0,
∴lnx1+lnx2=a(x1+x2),lnx1-lnx2=a(x1-x2),
∴a(x1+x2)>2?
| lnx1-lnx2 |
| x1-x2 |
| 2 |
| x1+x2 |
| x1 |
| x2 |
| 2(x1-x2) |
| x1+x2 |
令
| x1 |
| x2 |
| x1 |
| x2 |
| 2(x1-x2) |
| x1+x2 |
| 2(t-1) |
| t+1 |
设函数h(t)=lnt-
| 2(t-1) |
| t+1 |
| 1 |
| t |
| 4 |
| (t+1)2 |
| (t-1)2 |
| t(t+1)2 |
故函数h(t)在(1,+∞)上为增函数,∴h(t)>h(1)=0,
即不等式lnt>
| 2(t-1) |
| t+1 |
点评:1.本题主要考查导数的几何意义,利用导数研究函数的单调性、极值,考查的思想方法有分类讨论,转化与化归,数形结合,函数与方程思想等,综合性强,属压轴题.
2.判断函数f(x)在某区间内的零点个数,常用如下两种方式处理:
(1)利用导数判断函数的单调性,求出单调区间、极值与极值点、端点处的函数值,再根据零点存在性定理或零点唯一性定理判断.
(2)令f(x)=0,将方程变形,把等式两边各看作一个函数,从而将零点问题转化为两函数图象的交点问题.
3.利用导数证明不等式,是高考的热点之一,关键是构造适当的函数,判断区间端点对应的函数值与0的关系.
运用导数证明不等式f(x)>g(x)成立的一般步骤是:
(1)构造函数h(x)=f(x)-g(x);
(2)求h'(x);
(3)判断h(x)的单调性,
(4)求h(x)的最小值或值域;
(5)证明[h(x)]min>0成立;
(6)从而得出结论.
2.判断函数f(x)在某区间内的零点个数,常用如下两种方式处理:
(1)利用导数判断函数的单调性,求出单调区间、极值与极值点、端点处的函数值,再根据零点存在性定理或零点唯一性定理判断.
(2)令f(x)=0,将方程变形,把等式两边各看作一个函数,从而将零点问题转化为两函数图象的交点问题.
3.利用导数证明不等式,是高考的热点之一,关键是构造适当的函数,判断区间端点对应的函数值与0的关系.
运用导数证明不等式f(x)>g(x)成立的一般步骤是:
(1)构造函数h(x)=f(x)-g(x);
(2)求h'(x);
(3)判断h(x)的单调性,
(4)求h(x)的最小值或值域;
(5)证明[h(x)]min>0成立;
(6)从而得出结论.

练习册系列答案
相关题目
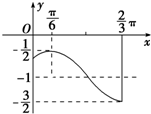 如图,是函数y=Asin(ωx+φ)+k(A>0,ω>0)的一段图象.
如图,是函数y=Asin(ωx+φ)+k(A>0,ω>0)的一段图象.