题目内容

（1）化简：
sin(α+
π
4
)
2cos2
α
2
+2sin
α
2
cos
α
2
-1

（2）若tanα=-3，求
sinα+2cosα
5cosα-sinα
的值．
考点：二倍角的余弦,三角函数的化简求值,两角和与差的正弦函数
专题：计算题,三角函数的求值
分析：（1）将分母化简或将分子展开，即可得出结论；
（2）先弦化切，再代入计算即可．
解答： 解：（1）
sin(α+
π
4
)
2cos2
α
2
+2sin
α
2
cos
α
2
-1
=
sin(α+
π
4
)
sinα+cosα
=
sin(α+
π
4
)
2
sin(α+
π
4
)
=
2
2
；
（2）
sinα+2cosα
5cosα-sinα
=
sinα
cosα
+2
5-
sinα
cosα
=
tanα+2
5-tanα
=
-3+2
5-(-3)
=-
1
8
．
点评：本题考查三角函数的化简求值，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
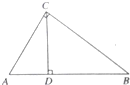如图，在△ABC中，∠ACB=90°，CD⊥AB，D为垂足，若CD=6cm，AD：DB=1：2，则AD的值是（　　）
A、6cm
B、3
2
cm
C、18cm
D、3
6
cm
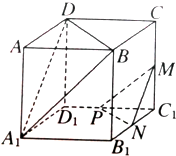在如图所示的正方体ABCD-A1B1C1D1中．
（Ⅰ）若M、N、P分别是C1C、B1C1、D1C1的中点，求证：平面MNP∥平面A1BD．
（Ⅱ）求直线BC1与平面ACC1A1所成角的大小．
已知复数z1=a-4i，z2=8+6i，
z1
z2
为纯虚数．
（Ⅰ）求实数a的值；
（Ⅱ）求复数z1的平方根．
在△ABC中，a，b，c成等比数列，
（1）若B是A和C的等差中项，求A；
（2）若b=1，求△ABC的面积的最大值．
如图，在边长为4的菱形ABCD中，∠DAB=60°．点E、F分别在边CD、CB上，点E与点C、D不重合，EF⊥AC，EF∩AC=O．沿EF将△CEF翻折到△PEF的位置，使平面PEF⊥平面ABFED，点Q满足
AQ
=λ
QP
（λ＞0）．
（1）求证：BD⊥平面POA；
（2）求PB的最小值，并探究此时直线OQ与平面PBD所成的角是否一定大于
π
4
？
设函数f（x）=ax5+bx3+c的图象过点（0，1），当x=1取得极值
13
15
．
（1）求f（x）；
（2）求f（x）的单调区间和极值．
有甲乙两个班级进行数学考试，按照大于等于85分为优秀，85分以下为非优秀统计成绩后，得到如下的列联表．
优秀 非优秀 总计
甲班 10
乙班 30
合计 105
已知在全部105人中抽到随机抽取1人为优秀的概率为
2
7

（Ⅰ）请完成上面的列联表；
（Ⅱ）根据列联表的数据，若按95%的可靠性要求，能否认为“成绩与班级有关系”．
设a∈R，函数f（x）=lnx-ax．
（1）若a=2，求曲线y=f（x）在x=1处的切线方程；
（2）若a＜
2
e2
，试判断函数f（x）在x∈（1，e2）的零点个数，并说明你的理由；
（3）若f（x）有两个相异零点x1，x2，求证：x1•x2＞e2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网