题目内容
6.已知函数f(x)=-$\frac{1}{2}$x2+4x-3lnx在(t,t+1)上存在极值点,则实数t的取值范围是(0,1)∪(2,3).分析 先求解导函数f′(x),再由“函数f(x)=-$\frac{1}{2}$x2+4x-3lnx在(t,t+1)上存在极值点”,转化为“f′(x)=0在区间(t,t+1)上有解”,进而求出答案.
解答 解:∵函数f(x)=-$\frac{1}{2}$x2+4x-3lnx,可知x>0,
∴f′(x)=-x+4$-\frac{3}{x}$,
∵函数f(x)=-$\frac{1}{2}$x2+4x-3lnx在(t,t+1)上存在极值点,
∴f′′(x)=-x+4$-\frac{3}{x}$=0在(t,t+1)上有解
∴$\frac{{x}^{2}-4x+3}{x}$=0在(t,t+1)上有解
∴g(x)=x2-4x+3=0在(t,t+1)上有解,
由x2-4x+3=0得:x=1,或x=3,
∴1∈(t,t+1),
即t∈(0,1),
∴3∈(t,t+1),
即t∈(2,3),
故实数t的取值范围是(0,1)∪(2,3),
故答案为:(0,1)∪(2,3).
点评 本题主要考查导数法研究函数的单调性,基本思路:当函数是增函数时,导数大于等于零恒成立,当函数是减函数时,导数小于等于零恒成立,然后转化为求相应函数的最值问题.注意判别式的应用.

练习册系列答案
相关题目
16.若函数f(x)=x2-2lnx在x=x0处的切线与直线x+3y+2=0垂直,则x0=( )
| A. | $-\frac{1}{2}$或2 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
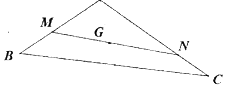 如图,已知点G是△ABC的重心,过点G作直线与AB、AC两边分别交于M、N两点,且$\overrightarrow{AM}$=$\frac{a}{3}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{b}{6}$$\overrightarrow{AC}$,则$\frac{2}{a-1}$+$\frac{1}{b-2}$的最小值为3.
如图,已知点G是△ABC的重心,过点G作直线与AB、AC两边分别交于M、N两点,且$\overrightarrow{AM}$=$\frac{a}{3}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{b}{6}$$\overrightarrow{AC}$,则$\frac{2}{a-1}$+$\frac{1}{b-2}$的最小值为3.