题目内容
7.将函数f(x)=sin2x的图象向右平移φ(0<φ<$\frac{π}{2}$)个单位后得g(x)的图象,若对满足f(x1)•g(x2)=-1的任意x1,x2,都有|x1-x2|min=$\frac{π}{4}$,则φ的值为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{5π}{12}$ | D. | $\frac{π}{3}$ |
分析 根据函数平移关系求出函数g(x)的解析式,根据条件对满足f(x1)•g(x2)=-1的任意x1,x2,都有|x1-x2|min=$\frac{π}{4}$,建立方程关系进行求解即可.
解答 解:将函数f(x)=sin2x的图象向右平移φ(0<φ<$\frac{π}{2}$)个单位后得g(x)的图象,
则g(x)=sin2(x-φ)=sin(2x-2φ),
则由f(x1)•g(x2)=-1得sin2x1•sin(2x2-2φ)=-1,
则sin2x1=1,且sin(2x2-2φ)=-1,或sin2x1=-1,且sin(2x2-2φ)=1,
根据对称性不妨取sin2x1=1,且sin(2x2-2φ)=-1,
则2x1=$\frac{π}{2}$+2k1π,2x2-2φ=-$\frac{π}{2}$+2k2π,
得x1=$\frac{π}{4}$+k1π,x2=φ-$\frac{π}{4}$+k2π,
则x1-x2=$\frac{π}{4}$+k1π,-φ+$\frac{π}{4}$-k2π=$\frac{π}{2}$-φ+(k1-k2)π,
∵|x1-x2|min=$\frac{π}{4}$,
∴|$\frac{π}{2}$-φ+(k1-k2)π|min=$\frac{π}{4}$,
∵0<φ<$\frac{π}{2}$,∴当(k1-k2)π=0时,$\frac{π}{2}$-φ=$\frac{π}{4}$,得φ=$\frac{π}{4}$,
故选:B.
点评 本题主要考查三角函数的图象和性质,结合三角函数的图象平移关系求出函数的解析式是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
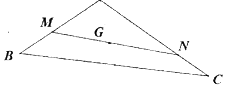 如图,已知点G是△ABC的重心,过点G作直线与AB、AC两边分别交于M、N两点,且$\overrightarrow{AM}$=$\frac{a}{3}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{b}{6}$$\overrightarrow{AC}$,则$\frac{2}{a-1}$+$\frac{1}{b-2}$的最小值为3.
如图,已知点G是△ABC的重心,过点G作直线与AB、AC两边分别交于M、N两点,且$\overrightarrow{AM}$=$\frac{a}{3}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{b}{6}$$\overrightarrow{AC}$,则$\frac{2}{a-1}$+$\frac{1}{b-2}$的最小值为3.