��Ŀ����
4��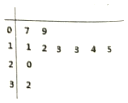 Ϊ���������������ˮ��ij�о���ȫ��ʵʩ����ˮ�ۣ�����ˮ��ԭ������סլ��һ��סլΪһ����������ˮ��Ϊ�����ۣ����廮�ֱ������
Ϊ���������������ˮ��ij�о���ȫ��ʵʩ����ˮ�ۣ�����ˮ��ԭ������סլ��һ��סլΪһ����������ˮ��Ϊ�����ۣ����廮�ֱ������| ���ݼ��� | ��һ����ˮ���� | �ڶ�����ˮ���� | ��������ˮ���� |
| ������ˮ����Χ����λ�������ף� | ��0��10] | ��10��15] | ����15��+�ޣ� |
��1����Ҫ����10����ͥ������ѡȡ3������ȡ���ڶ�����ˮ���Ļ����ķֲ��к;�ֵ��
��2���ó鵽��10����ͥ��Ϊ��������ȫ�еľ�����ˮ�������ȫ�����������ȡ10�������鵽n������ˮ��Ϊ�ڶ�����ˮ���Ŀ�����������n��ֵ��
���� ��1���ɾ�Ҷͼ��֪����ȡ��10������ˮ��Ϊһ����2����������6����������2����ȡ���ڶ�����ˮ���Ļ���X��ȡֵ����Ϊ0��1��2��3������P��X=k��=$\frac{{∁}_{4}^{3-k}{∁}_{6}^{k}}{{∁}_{10}^{3}}$���ɵ�X�ĸ��ʷֲ��м�����ѧ������
��2�����ȫ�����������ȡ10�����鵽Y������ˮ��Ϊ�ڶ�����ˮ������Y��B$��10��\frac{3}{5}��$��P��Y=k��=${∁}_{10}^{k}��\frac{3}{5}��^{k}��\frac{2}{5}��^{10-k}$��k=0��1��2������10������t=$\frac{P��Y=k��}{P��Y=k-1��}$=$\frac{3��11-k��}{2k}$����t��1���ɵ�k��6.6��P��Y=k-1����P��Y=k-1������t��1����k��6.6��P��Y=k-1����P��Y=k-1�������ɵó���
��� �⣺��1���ɾ�Ҷͼ��֪����ȡ��10������ˮ��Ϊһ����2����������6����������2����ȡ���ڶ�����ˮ���Ļ���X��ȡֵ����Ϊ0��1��2��3����P��X=k��=$\frac{{∁}_{4}^{3-k}{∁}_{6}^{k}}{{∁}_{10}^{3}}$���ɵã�P��X=0��=$\frac{1}{30}$��P��X=1��=$\frac{3}{10}$��P��X=2��=$\frac{1}{2}$��
P��X=3��=$\frac{1}{6}$��
�ɵ�X�ֲ���Ϊ��
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{30}$ | $\frac{3}{10}$ | $\frac{1}{2}$ | $\frac{1}{6}$ |
��2�����ȫ�����������ȡ10�����鵽Y������ˮ��Ϊ�ڶ�����ˮ������Y��B$��10��\frac{3}{5}��$��
P��Y=k��=${∁}_{10}^{k}��\frac{3}{5}��^{k}��\frac{2}{5}��^{10-k}$��k=0��1��2������10����
��t=$\frac{P��Y=k��}{P��Y=k-1��}$=$\frac{3��11-k��}{2k}$��
��t��1����k��6.6��P��Y=k-1����P��Y=k-1������t��1����k��6.6��P��Y=k-1����P��Y=k-1����
kȡ6����7�Ŀ����ԱȽϴ�
������֤k=6ʱ��$\frac{P��Y=6��}{P��Y=7��}$=$\frac{7}{6}$��1����n=6��
���� ���⿼���˾�Ҷͼ�����ʼ���Ӧ�á������ηֲ��������ֲ��еĸ��ʼ�������ѧ�������㹫ʽ��������ļ��㹫ʽ������ʽ�����ʣ�������������������������������е��⣮

| A�� | 2 | B�� | -2 | C�� | 3 | D�� | -3 |
| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
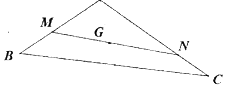 ��ͼ����֪��G�ǡ�ABC�����ģ�����G��ֱ����AB��AC���߷ֱ���M��N���㣬��$\overrightarrow{AM}$=$\frac{a}{3}$$\overrightarrow{AB}$��$\overrightarrow{AN}$=$\frac{b}{6}$$\overrightarrow{AC}$����$\frac{2}{a-1}$+$\frac{1}{b-2}$����СֵΪ3��
��ͼ����֪��G�ǡ�ABC�����ģ�����G��ֱ����AB��AC���߷ֱ���M��N���㣬��$\overrightarrow{AM}$=$\frac{a}{3}$$\overrightarrow{AB}$��$\overrightarrow{AN}$=$\frac{b}{6}$$\overrightarrow{AC}$����$\frac{2}{a-1}$+$\frac{1}{b-2}$����СֵΪ3��