题目内容
在区间(0,+∞)内为增函数的是( )
A、y=
| ||
B、y=(
| ||
C、y=log
| ||
| D、y=lgx |
考点:函数的单调性及单调区间
专题:计算题,函数的性质及应用
分析:运用常见函数的单调性,即可得到在区间(0,+∞)内为增函数的函数.
解答:
解:对于A.则为反比例函数,在x>0上为减函数,则A不满足条件;
对于B.则为底数小于1的指数函数,在R上递减,则B不满足条件;
对于C.为底数小于1的对数函数,在x>0上递减,则C不满足条件;
对于D.为10为底的对数函数,在x>0上递增,则D满足条件.
故选D.
对于B.则为底数小于1的指数函数,在R上递减,则B不满足条件;
对于C.为底数小于1的对数函数,在x>0上递减,则C不满足条件;
对于D.为10为底的对数函数,在x>0上递增,则D满足条件.
故选D.
点评:本题考查函数的单调性的判断,考查常见函数的单调性,考查判断能力,属于基础题.

练习册系列答案
相关题目
函数f(x)=x
-
的零点所在的区间是( )
| 1 |
| 3 |
| 1 |
| 2x |
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
已知函数y=f(x)-1为奇函数,且f(x)的最大值为M,最小值为N,则有( )
| A、M-N=4 |
| B、M-N=2 |
| C、M+N=2 |
| D、M+N=4 |
集合M={x|x-2=0},N={x|x>1},则( )
| A、M=N | B、M⊆N |
| C、M?N | D、M与N无包含关系 |
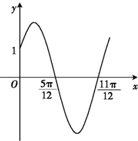 已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<