题目内容
若复数z与（z-1）2-2i都是纯虚数，则z=（ ）
| A、i | B、-i | C、±i | D、1 |
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：利用复数的运算法则、纯虚数的定义即可得出．
解答：
解：∵复数z与（z-1）2-2i都是纯虚数，
∴可设z=bi（b∈R，b≠0），
（z-1）2-2i=1-2bi-b2-2i=（1-b2）-（2b+2）i，
∴
，解得b=1．
∴z=i．
故选：A．
∴可设z=bi（b∈R，b≠0），
（z-1）2-2i=1-2bi-b2-2i=（1-b2）-（2b+2）i，
∴
|
∴z=i．
故选：A．
点评：本题考查了复数的运算法则、纯虚数的定义，考查了计算能力，属于基础题．
练习册系列答案
期末集结号系列答案
相关题目
已知函数f（x）=cos
x，f（x）=a在区间（
，2π）上恰有三个不同的实数根，且三个实数根从小到大依次成等比数列，则这三个实数根之和为（ ）
| 3 |
| 2 |
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
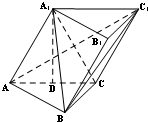如图所示，已知三棱柱ABC-A1B1C1，点A1在底面ABC上的射影恰为AC的中点D，∠BCA=90°，AC=BC=2，BA1⊥AC1．
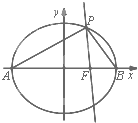已知椭圆C的中心在坐标原点，右焦点为F（1，0），A，B是椭圆的左、右顶点，P是椭圆C上异于A，B的动点，且△APB面积的最大值为