题目内容
已知角α的顶点与原点重合,始边与x轴的非负半轴重合,终边落在射线3x+4y=0(x<0)上,则2sinα+cosα的值为 .
考点:任意角的三角函数的定义
专题:三角函数的求值
分析:在角α的终边上任意取一点P(-4a,3a),a>0,由任意角的三角函数的定义求得sinα=
和cosα=
的值,从而求得2sinα+cosα 的值.
| y |
| r |
| x |
| r |
解答:
解:根据角α的终边落在射线3x+4y=0(x<0)上,在角α的终边上任意取一点P(-4a,3a),a>0,
则r=|OP|=
=5a,∴sinα=
=
=
,cosα=
=
=-
,
故2sinα+cosα=
-
=
,
故答案为:
.
则r=|OP|=
| 16a2+9a2 |
| y |
| r |
| 3a |
| 5a |
| 3 |
| 5 |
| x |
| r |
| -4a |
| 5a |
| 4 |
| 5 |
故2sinα+cosα=
| 6 |
| 5 |
| 4 |
| 5 |
| 2 |
| 5 |
故答案为:
| 2 |
| 5 |
点评:本题主要考查任意角的三角函数的定义,两点间的距离公式的应用,属于基础题.

练习册系列答案
相关题目
若f(x)=(m-1)x2+2mx+3为偶函数,则f(x)在区间(-7,-2)上是( )
| A、减函数 | B、先减后增函数 |
| C、增函数 | D、先增后减函数 |
已知等差数列{an}的公差为2,若a1,a3和a4成等比数列,则a1可以等于( )
| A、-4 | B、-6 | C、-8 | D、-10 |
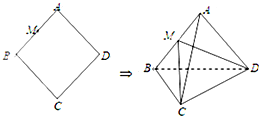 在边长为5的菱形ABCD中,AC=8,现沿对角线BD把△ABD折起,折起后使∠ADC的余弦值为
在边长为5的菱形ABCD中,AC=8,现沿对角线BD把△ABD折起,折起后使∠ADC的余弦值为