已知函数f(x)的部分图象如图所示.向图中的矩形区域随机投出100粒豆子.记下落入阴影区域的豆子数．通过10次这样的试验.算得落入阴影区域的豆子的平均数约为39.由此可估计$\int\begin{array}{l}1\\ 0\end{array}fA．$\frac{61}{100}$B．$\frac{39}{100}$C．$\frac{10}{100}$D．$\ 题目和参考答案——青夏教育精英家教网—

题目内容

11．

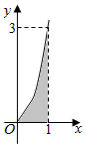已知函数f（x）的部分图象如图所示，向图中的矩形区域随机投出100粒豆子，记下落入阴影区域的豆子数．通过10次这样的试验，算得落入阴影区域的豆子的平均数约为39，由此可估计$\int\begin{array}{l}1\\ 0\end{array}f（x）dx$的值约为（　　）

A．

$\frac{61}{100}$

B．

$\frac{39}{100}$

C．

$\frac{10}{100}$

D．

$\frac{117}{100}$

分析利用阴影部分与矩形的面积比等于落入阴影部分的豆子数与所有豆子数的比，由此求出阴影部分的面积

解答解：由题意设阴影部分的面积为S，则$\frac{S}{3}$=$\frac{39}{100}$，所以S=$\frac{117}{100}$；
故选：D．

点评本题考查了几何概型的应用；关键是明确落入阴影部分的豆子数与所有豆子的比等于阴影部分与矩形的面积比．

练习册系列答案

2．等差数列{a_n}中，已知a₂≥5，a₃≤3，则a₅能取得最大（大或小）值为-1．

19．已知集合A={y|y=2^x-1，x∈R}，B={x|x≥2}，则（　　）

6．已知满足线性相关关系的两个变量x，y的取值如表：

x	0	1	3	4
y	2.2	4.3	4.8	6.7

若回归直线方程为$\hat y=0.95x+a$，则a=（　　）

16．设曲线$y=\sqrt{2x-{x^2}}$与x轴所围成的区域为D，向区域D内随机投一点，则该点落入区域{（x，y）∈D|x²+y²＜2}内的概率为$\frac{π-1}{π}$．

3．设集合A={x|-2＜x＜0}，B={x|-1＜x＜1}，则A∪B={x|-2＜x＜1}．

20．若（3x-$\frac{1}{x}$）ⁿ展开式中各项系数之和为16，则展开式中含x²项的系数为-108．

1．直角梯形ABCD满足AB∥CD，AD=CD=$\frac{1}{2}$AB=1，AD⊥AB，点M是梯形边上的任意一点．则AM≥$\sqrt{2}$的概率是（　　）

A．

$\frac{4+\sqrt{2}}{7}$

B．

$\frac{4-\sqrt{2}}{7}$

C．

$\frac{4+\sqrt{2}}{8}$

D．

$\frac{4-\sqrt{2}}{8}$

试题分类