题目内容
2．等差数列{an}中，已知a2≥5，a3≤3，则a5能取得最大（大或小）值为-1．分析 利用等差列的通项公式求解．
解答 解：∵等差数列{an}中，a2≥5，a3≤3，
∴$\left\{\begin{array}{l}{{a}_{1}+d≥5}\\{{a}_{1}+2d≤3}\end{array}\right.$，∴5-d≤a1≤3-2d，
∴5-d≤3-2d，解得d≤-2
5+3d≤a5=a1+4d≤3+2d，
∴a5能取得最大值为3+2d≤3-4=-1．
∴a5能取得最大值-1．
故答案为：大，-1．
点评 本题考查等差数列的第5项的最值的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
相关题目
10．在平面直角坐标系xOy中，已知点A、B分别在x、y轴上运动，且|AB|=2，若$\overrightarrow m=\frac{1}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}$，则$|\overrightarrow m|$的取值范围是（ ）
| A． | $[\frac{2}{3}，\frac{4}{3}]$ | B． | $[\frac{1}{3}，\frac{2}{3}]$ | C． | [0，2] | D． | $[0，\frac{{2\sqrt{5}}}{3}]$ |
17．4名同学参加3项不同的课外活动，若每名同学可自由选择参加其中的一项，则每项活动至少有一名同学参加的概率为（ ）
| A． | $\frac{4}{9}$ | B． | $\frac{4}{27}$ | C． | $\frac{9}{64}$ | D． | $\frac{3}{64}$ |
7．4sin40°-tan40°的值为（ ）
| A． | $\sqrt{3}$ | B． | $\sqrt{2}$ | C． | $\frac{{\sqrt{2}+\sqrt{3}}}{2}$ | D． | 2$\sqrt{2}$-1 |
14．已知点（x，y）满足不等式组$\left\{\begin{array}{l}{x-4y+3≤0}\\{2x-y-1≥0}\\{3x+2y-19≤0}\end{array}\right.$，则z=x-2y的最大值为（ ）
| A． | -7 | B． | -1 | C． | 1 | D． | 2 |
11．
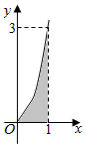已知函数f（x）的部分图象如图所示，向图中的矩形区域随机投出100粒豆子，记下落入阴影区域的豆子数．通过10次这样的试验，算得落入阴影区域的豆子的平均数约为39，由此可估计$\int\begin{array}{l}1\\ 0\end{array}f（x）dx$的值约为（ ）
已知函数f（x）的部分图象如图所示，向图中的矩形区域随机投出100粒豆子，记下落入阴影区域的豆子数．通过10次这样的试验，算得落入阴影区域的豆子的平均数约为39，由此可估计$\int\begin{array}{l}1\\ 0\end{array}f（x）dx$的值约为（ ）| A． | $\frac{61}{100}$ | B． | $\frac{39}{100}$ | C． | $\frac{10}{100}$ | D． | $\frac{117}{100}$ |