题目内容
16.设曲线$y=\sqrt{2x-{x^2}}$与x轴所围成的区域为D,向区域D内随机投一点,则该点落入区域{(x,y)∈D|x2+y2<2}内的概率为$\frac{π-1}{π}$.分析 求出对应区域的面积,利用几何概型的概率公式进行计算即可得到结论.
解答 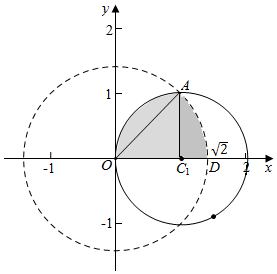 解:$y=\sqrt{2x-{x^2}}$与x轴所围成的区域为以C(1,0)为圆心半径为1的上半圆,面积SD=$\frac{1}{2}π×{1}^{2}$=$\frac{π}{2}$,
解:$y=\sqrt{2x-{x^2}}$与x轴所围成的区域为以C(1,0)为圆心半径为1的上半圆,面积SD=$\frac{1}{2}π×{1}^{2}$=$\frac{π}{2}$,
该点落入区域{(x,y)∈D|x2+y2<2}的区域如图:如图阴影部分,
则扇形AOC的面积S=$\frac{1}{4}π×{1}^{2}$=$\frac{π}{4}$,
三角形OAC的面积S△AOC=$\frac{1}{2}×1×1$=$\frac{1}{2}$,
扇形AOD的面积S=$\frac{45}{360}$π$(\sqrt{2})^{2}$=$\frac{π}{4}$,
则阴影部分的面积S阴影=S扇形AOC+S扇形AOD-S△AOC=$\frac{π}{4}$+$\frac{π}{4}$-$\frac{1}{2}$=$\frac{π}{2}$-$\frac{1}{2}$,
由几何概率的计算公式可得,该点落入区域{(x,y)∈D|x2+y2<2}的概率P=$\frac{\frac{π-1}{2}}{\frac{π}{2}}$=$\frac{π-1}{π}$,
故答案为:$\frac{π-1}{π}$.
点评 本题主要考查了几何概型的概率计算以及扇形的面积公式的计算,要求熟练掌握扇形的面积公式和几何概型的概率公式.

练习册系列答案
相关题目
7.4sin40°-tan40°的值为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{2}+\sqrt{3}}}{2}$ | D. | 2$\sqrt{2}$-1 |
4.设全集U=R,集合P={x|x>2},Q={x|x2-x-2<0},则(∁UP)∩Q=( )
| A. | (-1,2) | B. | (-1,2] | C. | (-2,1) | D. | ∅ |
11.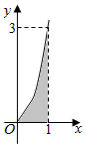 已知函数f(x)的部分图象如图所示,向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为39,由此可估计$\int\begin{array}{l}1\\ 0\end{array}f(x)dx$的值约为( )
已知函数f(x)的部分图象如图所示,向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为39,由此可估计$\int\begin{array}{l}1\\ 0\end{array}f(x)dx$的值约为( )
 已知函数f(x)的部分图象如图所示,向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为39,由此可估计$\int\begin{array}{l}1\\ 0\end{array}f(x)dx$的值约为( )
已知函数f(x)的部分图象如图所示,向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为39,由此可估计$\int\begin{array}{l}1\\ 0\end{array}f(x)dx$的值约为( )| A. | $\frac{61}{100}$ | B. | $\frac{39}{100}$ | C. | $\frac{10}{100}$ | D. | $\frac{117}{100}$ |
1.下列函数中,在定义域内是偶函数,且值域为[0,+∞)的是( )
| A. | f(x)=x2 | B. | f(x)=2x-1 | C. | f(x)=x2+cosx | D. | f(x)=xsinx |
8.实数a,b,则(a+b)(1+a)>0,是$\frac{1-b}{1+a}$<1恒成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |