题目内容
20.若(3x-$\frac{1}{x}$)n展开式中各项系数之和为16,则展开式中含x2项的系数为-108.分析 先求出二项式的指数n,再利用展开式的通项公式求出展开式中含x2项的系数.
解答 解:因为(3x-$\frac{1}{x}$)n展开式中各项系数之和为16,
令x=1,得出(3×1-$\frac{1}{1}$)n=16,
解得n=4;
所以(3x-$\frac{1}{x}$)4 展开式的通项公式为:
Tr+1=${C}_{4}^{r}$•(3x)4-r•${(-\frac{1}{x})}^{r}$=(-1)r•34-r•x4-2r,
当4-2r=2时,解得r=1,
所以展开式中含 x2项的系数为:
(-1)1C4333=-108.
故答案为:-108.
点评 本题考查了二项式展开式中各项系数之和与通项公式的应用问题,是基础题目.

练习册系列答案
相关题目
10.在平面直角坐标系xOy中,已知点A、B分别在x、y轴上运动,且|AB|=2,若$\overrightarrow m=\frac{1}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}$,则$|\overrightarrow m|$的取值范围是( )
| A. | $[\frac{2}{3},\frac{4}{3}]$ | B. | $[\frac{1}{3},\frac{2}{3}]$ | C. | [0,2] | D. | $[0,\frac{{2\sqrt{5}}}{3}]$ |
11.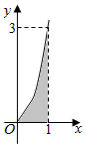 已知函数f(x)的部分图象如图所示,向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为39,由此可估计$\int\begin{array}{l}1\\ 0\end{array}f(x)dx$的值约为( )
已知函数f(x)的部分图象如图所示,向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为39,由此可估计$\int\begin{array}{l}1\\ 0\end{array}f(x)dx$的值约为( )
 已知函数f(x)的部分图象如图所示,向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为39,由此可估计$\int\begin{array}{l}1\\ 0\end{array}f(x)dx$的值约为( )
已知函数f(x)的部分图象如图所示,向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为39,由此可估计$\int\begin{array}{l}1\\ 0\end{array}f(x)dx$的值约为( )| A. | $\frac{61}{100}$ | B. | $\frac{39}{100}$ | C. | $\frac{10}{100}$ | D. | $\frac{117}{100}$ |
8.实数a,b,则(a+b)(1+a)>0,是$\frac{1-b}{1+a}$<1恒成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9.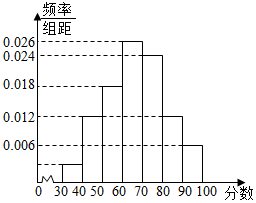 某校高二年级共有1600名学生,其中男生960名,640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在[80,100]的学生可取得A等(优秀),在[60,80)的学生可取得B等(良好),在[40,60)的学生可取得C等(合格),在不到40分的学生只能取得D等(不合格),为研究这次考试成绩优秀是否与性别有关,现按性别采用分层抽样的方法抽取100名学生,将他们的成绩按从低到高分成[30,40)、[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100]七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.
某校高二年级共有1600名学生,其中男生960名,640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在[80,100]的学生可取得A等(优秀),在[60,80)的学生可取得B等(良好),在[40,60)的学生可取得C等(合格),在不到40分的学生只能取得D等(不合格),为研究这次考试成绩优秀是否与性别有关,现按性别采用分层抽样的方法抽取100名学生,将他们的成绩按从低到高分成[30,40)、[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100]七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.
(Ⅰ)估计该校高二年级学生在正式的数学学业水平考试中,成绩不合格的人数;
(Ⅱ) 请你根据已知条件将下列2×2列联表补充完整,并判断是否有90%的把握认为“该校高二年级学生在本次考试中数学成绩优秀与性别有关”?
附:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$.
 某校高二年级共有1600名学生,其中男生960名,640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在[80,100]的学生可取得A等(优秀),在[60,80)的学生可取得B等(良好),在[40,60)的学生可取得C等(合格),在不到40分的学生只能取得D等(不合格),为研究这次考试成绩优秀是否与性别有关,现按性别采用分层抽样的方法抽取100名学生,将他们的成绩按从低到高分成[30,40)、[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100]七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.
某校高二年级共有1600名学生,其中男生960名,640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在[80,100]的学生可取得A等(优秀),在[60,80)的学生可取得B等(良好),在[40,60)的学生可取得C等(合格),在不到40分的学生只能取得D等(不合格),为研究这次考试成绩优秀是否与性别有关,现按性别采用分层抽样的方法抽取100名学生,将他们的成绩按从低到高分成[30,40)、[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100]七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.(Ⅰ)估计该校高二年级学生在正式的数学学业水平考试中,成绩不合格的人数;
(Ⅱ) 请你根据已知条件将下列2×2列联表补充完整,并判断是否有90%的把握认为“该校高二年级学生在本次考试中数学成绩优秀与性别有关”?
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 男生 | a=12 | b= | |
| 女生 | c= | d=34 | |
| 合计 | n=100 |
| P(k2≥k0) | 0.15 | 0.10 | 0.05 |
| k0 | 2.072 | 2.706 | 3.841 |