题目内容
已知共面向量
,
,
满足|
=|
|=1,<
,
>=120°且<
-
,
-
>=60°,则|
|的最大值为( )
| a |
| b |
| c |
| a| |
| b |
| a |
| b |
| a |
| c |
| b |
| c |
| c |
A、
| ||||
| B、1 | ||||
C、
| ||||
| D、2 |
考点:平面向量数量积的运算
专题:计算题,解三角形,平面向量及应用
分析:设
=
,
=
,
=
,利用向量的运算法则作出图;结合图,判断出四点共圆;利用正弦定理求出外接圆的直径,即为最大值.
| OA |
| a |
| OB |
| b |
| OC |
| c |
解答:
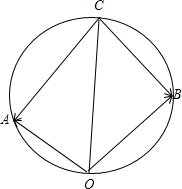 解:由|
解:由|
=|
|=1,<
,
>=120°,
且<
-
,
-
>=60°,
如图所示:设
=
,
=
,
=
,则
=
-
,
=
-
,
∴
=
-
,
2=
2+
2-2
•
=1+1-2×1×1×(-
)=3,
∴|
|=
,
由三角形的正弦定理得外接圆的直径2R=
=
=2,
当OC为直径时,它的模最大,且最大值为2,
故选:D.
 解:由|
解:由|| a| |
| b |
| a |
| b |
且<
| a |
| c |
| b |
| c |
如图所示:设
| OA |
| a |
| OB |
| b |
| OC |
| c |
| CA |
| a |
| c |
| CB |
| b |
| c |
∴
| AB |
| b |
| a |
| AB |
| b |
| a |
| a |
| b |
| 1 |
| 2 |
∴|
| AB |
| 3 |
由三角形的正弦定理得外接圆的直径2R=
| AB |
| sin∠ACB |
| ||
| sin60° |
当OC为直径时,它的模最大,且最大值为2,
故选:D.
点评:本题考查向量的数量积公式、向量的运算法则、四点共圆的判断、三角形的正弦定理,属于中档题.

练习册系列答案
相关题目
已知向量
,
满足
⊥
,|
|=1,|
|=2,则|2
-
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、2
| ||
B、2
| ||
| C、8 | ||
| D、12 |
设F为双曲线
-
=1(a>0,b>0)的右焦点,P是双曲线上的点,若它的渐近线上存在一点Q(在第一象限内),使得
=2
,则双曲线离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| FP |
| PQ |
| A、(1,3) |
| B、(3,+∞) |
| C、(1,2) |
| D、(2,+∞) |
若函数f(x)=
-
x2+x+1在区间(
,4)上有极值点,则实数a的取值范围是( )
| x3 |
| 3 |
| a |
| 2 |
| 1 |
| 3 |
A、(2,
| ||||
B、[2,
| ||||
C、(
| ||||
D、(2,
|
点A(1,3)关于直线y=kx+b的对称点是B(-2,1),则直线y=kx+b在x轴上的截距是( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
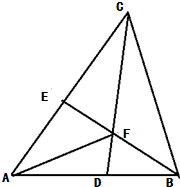 在△ABC中,∠A=60°,AB=3,AC=5,BD=1,CE=2.
在△ABC中,∠A=60°,AB=3,AC=5,BD=1,CE=2.