题目内容
设函数f（x）=
+a是奇函数（a为常数），则f（x）＜0的解集为（ ）
| 1 |
| 2x+1 |
| A、（0，+∞） | ||
| B、（1，+∞） | ||
| C、（-1，0）∪（0，1） | ||
D、（
|
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：函数f（x）=
+a是奇函数，可得f（0）=0，解出a，再利用不等式的性质、指数函数的单调性即可得出．
| 1 |
| 2x+1 |
解答：
解：∵函数f（x）=
+a是奇函数，
∴f（0）=0，
∴
+a=0，解得a=-
．
∴f（x）=
-
．
∵f（x）＜0，∴
-
＜0，
化为2x＞1，
解得x＞0．
∴f（x）＜0的解集为（0，+∞）．
故选：A．
| 1 |
| 2x+1 |
∴f（0）=0，
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴f（x）=
| 1 |
| 2x+1 |
| 1 |
| 2 |
∵f（x）＜0，∴
| 1 |
| 2x+1 |
| 1 |
| 2 |
化为2x＞1，
解得x＞0．
∴f（x）＜0的解集为（0，+∞）．
故选：A．
点评：本题考查了奇函数的性质、不等式的性质、指数函数的单调性，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
在正方体ABCD-A1B1C1D1中，若E是B1D1的中点，则直线BE垂直于（ ）
| A、AC |
| B、BD |
| C、A1D |
| D、A1D1 |
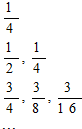如图给出了一个“直角三角形数阵”：满足每一列成等差数列，从第三行起，每一行的数成等比数列，且每一行的公比相等，记第i行第j列的数为aij（i≥j，i，j∈N*），则a88=