题目内容
已知函数f(x)=x2,定义域为[-2,1],值域为 .
考点:函数的值域
专题:函数的性质及应用
分析:先根据二次的对称轴及开口方向及对称轴,观察函数在给定区间上的单调性及最值点即可求得原函数的值域.
解答:
解:∵函数f(x)=x2-x+1的对称轴是:x=0,且开口向上,
∴函数f(x)=x2在定义域[-2,1]上的最大值为:yx=-2=4,
最小值为:yx=0=0,
故答案为:[0,4].
∴函数f(x)=x2在定义域[-2,1]上的最大值为:yx=-2=4,
最小值为:yx=0=0,
故答案为:[0,4].
点评:本题考查二次函数的值域,属于求二次函数的最值问题,考查运算求解能力,考查数形结合思想,属于基本题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知a,b,c分别为△ABC角A、B、C所对的边,若满足a=
,b=
,A=45°,则角B的大小为( )
| 2 |
| 3 |
| A、90° | B、60° |
| C、60°或120° | D、120° |
若a=
,b=3-
,c=log20.8,则( )
| 6 | 5 |
| 1 |
| 2 |
| A、a>b>c |
| B、b>a>c |
| C、c>a>b |
| D、b>c>a |
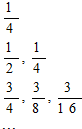 如图给出了一个“直角三角形数阵”:满足每一列成等差数列,从第三行起,每一行的数成等比数列,且每一行的公比相等,记第i行第j列的数为aij(i≥j,i,j∈N*),则a88=
如图给出了一个“直角三角形数阵”:满足每一列成等差数列,从第三行起,每一行的数成等比数列,且每一行的公比相等,记第i行第j列的数为aij(i≥j,i,j∈N*),则a88=