题目内容
16.已知函数f(x)=x3+ax2+bx+a2(a、b∈R)(1)若函数f(x)在x=1处有极值为10,求b的值;
(2)若a=-4,f(x)在x∈[0,2]上单调递增,求b的最小值.
分析 (1)先对函数求导f'(x)=3x2+2ax+b,由题意可得f(1)=10,f′(1)=0,结合导数存在的条件可求
(2)问题转化为b≥-3x2+8x在x∈[0,2]恒成立,从而有b≥(-3x2+8x)max,根据函数的单调性求出b的范围即可.
解答 解:(1)f'(x)=3x2+2ax+b,
若函数f(x)在x=1处有极值为10,
则 $\left\{\begin{array}{l}{f′(1)=3+2a+b=0}\\{f(1)=1+a+b{+a}^{2}=10}\end{array}\right.$⇒$\left\{\begin{array}{l}{a=4}\\{b=-11}\end{array}\right.$或 $\left\{\begin{array}{l}{a=-3}\\{b=3}\end{array}\right.$,
当 $\left\{\begin{array}{l}{a=4}\\{b=-11}\end{array}\right.$时,f'(x)=3x2+8x-11,
△=64+132>0,所以函数有极值点;
当 $\left\{\begin{array}{l}{a=-3}\\{b=3}\end{array}\right.$时,f′(x)=3(x-1)2≥0,
所以函数无极值点;
则b的值为-11.
(2)a=-4时,f(x)=x3-4x2+bx+16,
f'(x)=3x2-8x+b≥0对任意的x∈[0,2]都成立,
即b≥-3x2+8x,x∈[0,2],
令h(x)=-3x2+8x,对称轴x=$\frac{4}{3}$,
函数h(x)在[0,$\frac{4}{3}$)递增,在($\frac{4}{3}$,2]递减,
故h(x)max=h($\frac{4}{3}$)=$\frac{16}{3}$,
故b≥$\frac{16}{3}$,
则b的最小值为$\frac{16}{3}$.
点评 本题主要考查了利用导数研究函数的极值,利用构造函数的思想把恒成立转化为求解函数的最值问题,要注意构造思想在解题中的应用.

| A. | f(sinα)>f(cosβ) | B. | f(cosα)<f(cosβ) | C. | f(sinα)<f(cosβ) | D. | f(sinα)<f(sinβ) |
| A. | 2 | B. | -2 | C. | 8 | D. | -8 |
其中一定成立的关系式的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | (-∞,$\frac{1}{2}$]∪(1,+∞) | B. | [$\frac{1}{2}$,+∞) | C. | [$\frac{1}{2}$,1)∪(1,+∞) | D. | (-∞,$\frac{1}{2}$]∪[1,+∞) |
| A. | 25 | B. | 24 | C. | 21 | D. | 30 |
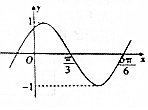 已知函数y=sin(ωx+φ)(ω>0,0<φ≤$\frac{π}{2}$)的部分图象如图所示,则cos(5ωφ)=-$\frac{1}{2}$.
已知函数y=sin(ωx+φ)(ω>0,0<φ≤$\frac{π}{2}$)的部分图象如图所示,则cos(5ωφ)=-$\frac{1}{2}$.