题目内容
在直角坐标系中,以原点为极点,x轴的正半轴为极轴建坐标系,已知曲线C:ρsin2θ=acosθ(a>0),已知过点P(-2,-4)的直线l的参数方程为:
,直线l与曲线C分别交于M,N两点.
(Ⅰ)写出曲线C和直线l的普通方程;
(Ⅱ)若a=2,求线段|MN|的长度.
|
(Ⅰ)写出曲线C和直线l的普通方程;
(Ⅱ)若a=2,求线段|MN|的长度.
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:本题(Ⅰ)利用极坐标方程普通方程的坐标关系式,将极坐标方程化成普通方程,通过消参数将参数方程化成普通方程;(Ⅱ)利用曲线C的普通方程和直线l的参数方程,求出相应的参数,利用参数差的绝对值得到MN的长度,即本题结论.
解答:
解:∵曲线C:ρsin2θ=acosθ(a>0),
∴(ρsinθ)2=2ρcsθ.
∵
∴y2=ax.
∵直线l的参数方程为:
(t为参数),
∴两式相关得减到y=x-2.
∴曲线C和直线l的普通方程分别为 y2=ax,y=x-2.
(Ⅱ)直线l的参数方程为:
(t为参数),
代入 y2=ax,得到t2-10
t+40=0.
则有t 1+t2=10
,t1t2=40.
∵|MN|=|t1-t2|,
∴|MN|2=(t1+t2)2-4t1t2=40.
解得|MN|=2
.
∴线段|MN|的长度为2
.
∴(ρsinθ)2=2ρcsθ.
∵
|
∴y2=ax.
∵直线l的参数方程为:
|
∴两式相关得减到y=x-2.
∴曲线C和直线l的普通方程分别为 y2=ax,y=x-2.
(Ⅱ)直线l的参数方程为:
|
代入 y2=ax,得到t2-10
| 2 |
则有t 1+t2=10
| 2 |
∵|MN|=|t1-t2|,
∴|MN|2=(t1+t2)2-4t1t2=40.
解得|MN|=2
| 10 |
∴线段|MN|的长度为2
| 10 |
点评:本题考查的是极坐标与参数方程的知识,计算量较大,属于中档题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
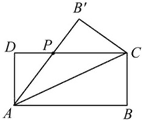 设矩形ABCD(AB>AD)的周长为24,把它关于AC折起来,AB折过去后交CD于点P,如图,设AB=x,求△ADP的面积的最大值,及此时x的值.
设矩形ABCD(AB>AD)的周长为24,把它关于AC折起来,AB折过去后交CD于点P,如图,设AB=x,求△ADP的面积的最大值,及此时x的值.