题目内容
如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=2,E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使得平面ABEF⊥平面EFDC.
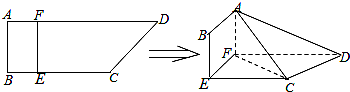
(Ⅰ)当BE=1,是否在折叠后的AD上存在一点P,且
=λ
,使得CP∥平面ABEF?若存在,求出λ的值;若不存在,说明理由;
(Ⅱ)设BE=x,问当x为何值时,三棱锥A-CDF的体积有最大值?并求出这个最大值.

(Ⅰ)当BE=1,是否在折叠后的AD上存在一点P,且
| AP |
| PD |
(Ⅱ)设BE=x,问当x为何值时,三棱锥A-CDF的体积有最大值?并求出这个最大值.
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(Ⅰ)根据CP∥平面ABEF的性质,建立条件关系即可得到结论.
(Ⅱ)设BE=x,根据三棱锥的体积公式即可得到结论.
(Ⅱ)设BE=x,根据三棱锥的体积公式即可得到结论.
解答:
解:(Ⅰ) 若存在P,使得CP∥平面ABEF,此时λ=
:
证明:当λ=
,此时
=
,可得
=
,
过P作MP∥FD,与AF交M,
则
=
,
又PD=5,故MP=3,
∵EC=3,MP∥FD∥EC,
∴MP∥EC,且MP=EC,故四边形MPCE为平行四边形,
∴PC∥ME,
∵CP?平面ABEF,ME?平面ABEF,
故答案为:CP∥平面ABEF成立.
(Ⅱ)∵平面ABEF⊥平面EFDC,ABEF∩平面EFDC=EF,AF⊥EF,
∴AF⊥平面EFDC,
∵BE=x,∴AF=x,(0<x<4),FD=6-x,
故三棱锥A-CDF的体积V=
×
×2×(6-x)x=
[-(x-3)2+9]=-
(x-3)2+3,
∴x=3时,三棱锥A-CDF的体积V有最大值,最大值为3.
| 3 |
| 2 |
证明:当λ=
| 3 |
| 2 |
| AP |
| 3 |
| 2 |
| PD |
| AP |
| AD |
| 3 |
| 5 |
过P作MP∥FD,与AF交M,
则
| MP |
| FD |
| 3 |
| 5 |

又PD=5,故MP=3,
∵EC=3,MP∥FD∥EC,
∴MP∥EC,且MP=EC,故四边形MPCE为平行四边形,
∴PC∥ME,
∵CP?平面ABEF,ME?平面ABEF,
故答案为:CP∥平面ABEF成立.
(Ⅱ)∵平面ABEF⊥平面EFDC,ABEF∩平面EFDC=EF,AF⊥EF,
∴AF⊥平面EFDC,
∵BE=x,∴AF=x,(0<x<4),FD=6-x,
故三棱锥A-CDF的体积V=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
∴x=3时,三棱锥A-CDF的体积V有最大值,最大值为3.
点评:本题主要考查直线和平面平行的性质和判定,以及三棱锥体积的计算,考查学生的推理能力.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
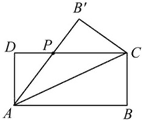 设矩形ABCD(AB>AD)的周长为24,把它关于AC折起来,AB折过去后交CD于点P,如图,设AB=x,求△ADP的面积的最大值,及此时x的值.
设矩形ABCD(AB>AD)的周长为24,把它关于AC折起来,AB折过去后交CD于点P,如图,设AB=x,求△ADP的面积的最大值,及此时x的值.