题目内容
如图，四棱锥S-ABCD的底面是正方形，SD⊥平面ABCD，SD=AD=a，点E是SD上的点，且DE=λa（0＜λ≤1）．（Ⅰ）求证：对任意的λ=（0，1]，都有AC⊥BE；
（Ⅱ）若二面角C-BE-A的大小为120°，求实数λ的值．
考点：二面角的平面角及求法,直线与平面垂直的性质,向量的数量积判断向量的共线与垂直
专题：空间位置关系与距离,空间角
分析：（I）以D为原点，DA，DC，DS为x，y，z轴，建立空间直角坐标系D-xyz，利用向量法能证明AC⊥BE恒成立．
（II）求出平面ABE的一个法向量和平面BCE的一个法向量，利用向量法能求出λ=1．
（II）求出平面ABE的一个法向量和平面BCE的一个法向量，利用向量法能求出λ=1．
解答：
（I）证明：以D为原点，DA，DC，DS为x，y，z轴，
如图建立空间直角坐标系D-xyz，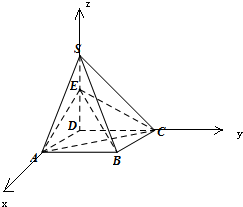
则A（a，0，0），B（a，a，0），
C（0，a，0），D（0，0，0），E（0，0，λa），
=(-a，a，0)，
=(-a，-a，λa)，…（3分）
∴
•
=0对任意λ∈（0，1]都成立，
即AC⊥BE恒成立．…（5分）
（II）解：设平面ABE的一个法向量为
=(x1，y1，z1)，
∵
=(0，a，0)，
=(-a，0，λa)，
∴
⇒
⇒
，
取z1=1，则x1=λ，
=(x1，y1，z1)=(λ，0，1)．…（7分）
设平面BCE的一个法向量为
=(x2，y2，z2)，
∵n=3n+1，∴n=
，
取z2=1，则y2=λ，
=(x2，y2，z2)，…（9分）
∵二面角C-AE-D的大小为120°，
∴cos?
，
＞=
=
=
， λ∈(0， 1]⇒λ=1，
∴λ=1为所求．…（12分）
如图建立空间直角坐标系D-xyz，
则A（a，0，0），B（a，a，0），
C（0，a，0），D（0，0，0），E（0，0，λa），
| AC |
| BE |
∴
| AC |
| BE |
即AC⊥BE恒成立．…（5分）
（II）解：设平面ABE的一个法向量为
| n1 |
∵
| AB |
| AE |
∴
|
|
|
取z1=1，则x1=λ，
| n1 |
设平面BCE的一个法向量为
| n2 |
∵n=3n+1，∴n=
| n |
| 2 |
取z2=1，则y2=λ，
| n2 |
∵二面角C-AE-D的大小为120°，
∴cos?
| n1 |
| n2 |
| ||||
|
|
| 1 |
| 1+λ2 |
| 1 |
| 2 |
∴λ=1为所求．…（12分）
点评：本题考查异面直线垂直的证明，考查使得二面角为120°的实数值的求法，是中档题，解题时要注意向量法的合理运用．
练习册系列答案
科学实验活动册系列答案
相关题目
在植物活动前为保证树苗的质量，林管部门会对树苗进行检测．先从甲、乙两种树苗中各抽测了10株树苗的高度，量出的高度（单位：厘米）制作成茎叶图如下，甲，乙两种树苗的平均高度分别记为| x |
| y |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f（x）=2sin（
-x）是（ ）
| π |
| 2 |
| A、最小正周期为2π的奇函数 |
| B、最小正周期为2π的偶函数 |
| C、最小正周期为π的奇函数 |
| D、最小正周期为4π的偶函数 |
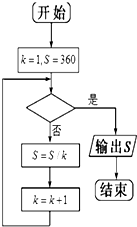执行如图所示的程序框图，运行的结果为S=3，那么判断框中应填入的关于k的判断条件是（ ）| A、k＞6？ | B、k＜6？ |
| C、k＞5？ | D、k＜5？ |