题目内容
7.定义在R上的奇函数f(x)满足f(x)=f(x+3),当x∈(0,$\frac{3}{2}$)时,f(x)=sin πx,且f($\frac{3}{2}$)=0,则函数f(x)在区间[-6,6]上的零点个数是( )| A. | 18 | B. | 17 | C. | 8 | D. | 9 |
分析 可判断f(x)的周期为3,作函数f(x)在[-$\frac{3}{2}$,$\frac{3}{2}$]上的图象,从而结合图象及周期性确定零点的个数.
解答 解:∵f(x)=f(x+3),
∴f(x)的周期为3,
∵当x∈(0,$\frac{3}{2}$)时,f(x)=sin πx,且f($\frac{3}{2}$)=0,且f(x)是奇函数;
∴作函数f(x)在[-$\frac{3}{2}$,$\frac{3}{2}$]上的图象如下,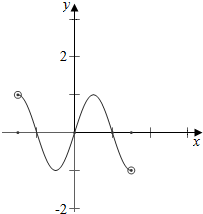 ,
,
结合图象可知,
f(-$\frac{3}{2}$)=f(-$\frac{9}{2}$)=f($\frac{3}{2}$)=f($\frac{9}{2}$)=0,
f(-1)=f(-4)=f(2)=f(5)=0,
f(1)=f(-2)=f(-5)=f(4)=0,
f(0)=f(-3)=f(-6)=f(3)=f(6)=0,
故函数f(x)在区间[-6,6]上的零点个数是17;
故选:B.
点评 本题考查了函数的零点的个数的判断及数形结合的思想应用.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
17.定义在R上的函数y=f(x)是奇函数,且x≥0时,f(x)=ln(x2-2x+2),则x<0时,f(x)的解析式是( )
| A. | f(x)=ln(-x2-2x+2) | B. | f(x)=ln(x2+2x+2) | C. | f(x)=-ln(-x2-2x+2) | D. | f(x)=-ln(x2+2x+2) |
15.已知点C(3,4),抛物线y2=8x的准线为L,设抛物线上任意一点P到直线L的距离为m,则m+|PC|的最小值为( )
| A. | 5 | B. | $\sqrt{41}$ | C. | $\sqrt{41}$-2 | D. | 4 |
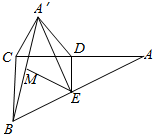 已知在△ABC中,D,E分别为AC,AB的中点,沿DE将△ADE折起,使A到A′的位置,若M是A′B的中点,求证:ME∥平面A′CD.
已知在△ABC中,D,E分别为AC,AB的中点,沿DE将△ADE折起,使A到A′的位置,若M是A′B的中点,求证:ME∥平面A′CD.