题目内容

若一个圆锥的侧面展开图是面积为2π的半圆面，则该圆锥的表面积为
 
．
考点：旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离
分析：由已知中圆锥的侧面展开图为半圆且面积为2π，我们易确定圆锥的母线长L与底面半径R之间的关系，进而求出侧面积S与底面面积之间的关系，即可得到结论．
解答： 解：设圆锥的母线长为L，底面半径为R
若圆锥的侧面展开图为半圆则
2πR=πL
即L=2R
又∵圆锥的侧面展开图为半圆且面积为2π，
则2π=
1
2
πL2=2πR2，圆锥的底面积为：πR2=π．
故其表面积为2π+π=3π
故答案为：3π．
点评：本题考查的知识点是圆锥的表面积，其中根据已知中圆锥的侧面展开图为半圆，确定圆锥的母线长与底面半径的关系是解答本题的关键．
练习册系列答案
相关题目
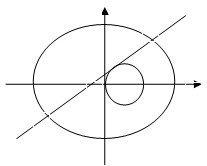已知中心在坐标原点，焦点在x轴上的椭圆过点P（2，
3
），且它的离心率e=
1
2
．
（1）求椭圆的标准方程；
（2）与圆（x-1）2+y2=1相切的直线l：y=kx+t交椭圆于M，N两点，若椭圆上一点C满足
OM
+
ON
=λ
OC
，求实数λ的取值范围．
在矩形ABCD中，AB=1，BC=
2
，PA⊥平面ABCD，PA=1，则PC与平面ABCD所成角是
 
．
若正三棱柱ABC-A1B1C1的棱长均相等，则AB1与侧面ACC1A1所成角的正切值为
 
．
二维空间中圆的二维度（面积）S=πr2，一维测度（周长）l=2πr； 三维空间中球的三维测度（体积）V=
4
3
πr3，二维测度（表面积）S=4πr2．若四维空间中“超球”的四维测度W=2πr4，根据上述规律，猜想其三维测度（体积）V=
 
．
若偶函数f（x）满足f（x+1）=f（x-1），且x∈[0，1]时，f（x）=
x
，则f（
7
2
）=
 
．
已知向量
a
=（x2，x+1），
b
=（1-x，t），若函数f（x）=
a
•
b
在区间（-1，1）上是增函数，则t的取值范围为
 
．
已知圆O：x2+y2=1，直线x-2y+5=0上动点P，过点P作圆O的一条切线，切点为A，则
PO
•
PA
的最小值为
 
．
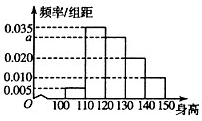从某小学随机抽取100名学生，将他们的身高（单位：厘米）数据绘制成频率分布直方图（如图），若要从身高在[120，130），[130，140），[140，150]三组内的学生中，用分层抽样的方法选取20人参加一项活动，则从身高在[120，130）内的学生中选取的人数应为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网