Question

数1，3，6，10，15，21…，这些数量的石子，都可以排成三角形，像这样的数称为三角形数．如图所示：

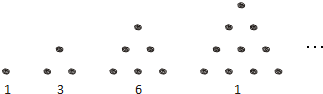
将三角形数1，3，6，10，…记为数列{a_n}，将可被5整除的三角形数按从小到大的顺序组成一个新数列{b_n}．可以推测：
（Ⅰ）b₂₀₁₄是数列{a_n}中的第

 

项；   
（Ⅱ）b_2k-1=

 

．（用k表示）．

Answer 1

考点：归纳推理

专题：规律型,点列、递归数列与数学归纳法

分析：（Ⅰ）通过归纳分析，三角形数是从l开始的连续自然数的和，得a_n=

n(n+1)

2

；
被5整除的数是5、10、15、20，…，第i个数是5i；
求出能同时满足两个式子的数，组成数列{b_n}．
（Ⅱ）由{b_2k-1}：10，45，105，190，…；归纳猜想b_2k-1=

5k(5k-1)

2

．

解答： 解：（Ⅰ）三角形数是从l开始的连续自然数的和，得a_n=

n(n+1)

2

n∈N^*；
被5整除的数是5、10、15、20，…，第i个数是5i，i∈N^*；
求出能同时满足两个式子的数，组成数列{b_n}：10，15，45，55，…，∴

n(n+1)

2

=5i
∴n（n+1）=10i
∴n=4，5，9，10，14，15，19，20，…；
又∵2014÷4=503…余数是2，
∴b₂₀₁₄=503×10+5=5035；
（Ⅱ）{b_2k-1}：10，45，105，190，…；
∴b_2k-1=

5k(5k-1)

2

．
故答案为：5035，

5k(5k-1)

2

．

点评：本题考查了数列的应用问题，也考查运算求解能力，推理论证能力，化归与转化思想；解题时应认真审题，注意总结规律，是综合题．