题目内容
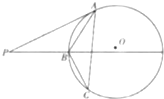如图，过圆O外一点P分别作圆的切线和割线交圆于A，B，且PB=9，C是圆上一点使得BC=4，∠BAC=∠APB，则AB=考点：圆的切线的性质定理的证明
专题：选作题,立体几何
分析：根据同弧所对的圆周角与弦切角相等，得到∠C=∠BAP，根据所给的两个角相等，得到两个三角形相似，根据相似三角形对应边成比例，得到比例式，代入已知的长度，求出结果．
解答：
解：∵∠BAC=∠APB，
∠C=∠BAP，
∴△PAB∽△ACB，
∴
=
∴AB2=PB•BC=9×4=36，
∴AB=6，
故答案为：6．
∠C=∠BAP，
∴△PAB∽△ACB，
∴
| PB |
| AB |
| AB |
| BC |
∴AB2=PB•BC=9×4=36，
∴AB=6，
故答案为：6．
点评：本题考查圆的切线的性质的应用，考查同弧所对的圆周角等于弦切角，考查三角形相似的判断和性质，本题是一个综合题目．
练习册系列答案
相关题目
如图所示，P是△ABC内一点，且满足
如图，设α∈（0，π），且α≠