题目内容
 如图,A(1,0),B(
如图,A(1,0),B(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
(1)求S=0的概率;
(2)求S的分布列与数学期望ES.
考点:离散型随机变量的期望与方差
专题:综合题,概率与统计
分析:(1)基本事件空间即从8个点中随机选取2个点共有
=28种取法,研究的事件即选取的2个点与原点在一个平面内的取法有4种,故由古典概型概率计算公式即可得所求;
(2)先确定随机变量S的所有可能取值,再利用古典概型概率计算公式分别计算随机变量取值的概率,最后列出分布列,利用期望计算公式计算S的期望.
| C | 2 8 |
(2)先确定随机变量S的所有可能取值,再利用古典概型概率计算公式分别计算随机变量取值的概率,最后列出分布列,利用期望计算公式计算S的期望.
解答:
解:(1)从8个点中随机选取2个点共有
=28种取法,选取的2个点与原点在一个平面内的取法有4种,
∴S=0的概率P(S=0)=
=
;
(2)S的所有可能取值为0,
,
,其中S=0有4种情况;S=
有16种情况;S=
有8种情况;
S的分布列
ES=0×
+
×
+
×
=
.
| C | 2 8 |
∴S=0的概率P(S=0)=
| 4 |
| 28 |
| 1 |
| 7 |
(2)S的所有可能取值为0,
| ||
| 4 |
| 1 |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
S的分布列
| S | 0 |
|
| ||||||
| P |
|
|
|
| 1 |
| 7 |
| ||
| 4 |
| 4 |
| 7 |
| 1 |
| 2 |
| 2 |
| 7 |
| ||
| 7 |
点评:本题主要考查了古典概型的概率的计算方法和计算公式,利用组合数公式进行计数的方法,离散型随机变量分布列的意义和期望的计算,属中档题.

练习册系列答案
相关题目
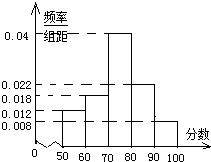 某次素质测试,随机抽取了部分学生的成绩,得到如图所示的频率分布直方图.
某次素质测试,随机抽取了部分学生的成绩,得到如图所示的频率分布直方图.