题目内容
已知f(x)=
(1)求函数f(x)的零点;
(2)解不等式f(x)<-3;
(3)求f(a+1)的值.
|
(1)求函数f(x)的零点;
(2)解不等式f(x)<-3;
(3)求f(a+1)的值.
考点:一元二次不等式的解法,函数的值,函数的零点
专题:综合题,函数的性质及应用
分析:(1)分x≥0、x<0两种情况讨论,分别解方程f(x)=0可得函数的零点;
(2)分x≥0、x<0两种情况讨论,分别解出不等式,然后取并集;
(3)分a+1≥0、a+1<0两种情况讨论,可求f(a+1)的值;
(2)分x≥0、x<0两种情况讨论,分别解出不等式,然后取并集;
(3)分a+1≥0、a+1<0两种情况讨论,可求f(a+1)的值;
解答:
解:(1)当x≥0时,f(x)=x(x-4),由f(x)=0解得x=0或4;
当x<0时,f(x)=x(x+4),由f(x)=0解得x=-4.
∴函数f(x)的零点为0,-4,4.
(2)当x≥0时,f(x)<-3即x(x-4)<-3,解得1<x<3;
当x<0时,f(x)<-3即x(x+4)<-3,解得-3<x<-1.
∴不等式f(x)<-3的解集为(-3,-1)∪(1,3).
(3)当a+1≥0,即a≥-1时,f(a+1)=(a+1)(a-3);
当a+1<0,即a<-1时,f(a+1)=(a+1)(a+5).
当x<0时,f(x)=x(x+4),由f(x)=0解得x=-4.
∴函数f(x)的零点为0,-4,4.
(2)当x≥0时,f(x)<-3即x(x-4)<-3,解得1<x<3;
当x<0时,f(x)<-3即x(x+4)<-3,解得-3<x<-1.
∴不等式f(x)<-3的解集为(-3,-1)∪(1,3).
(3)当a+1≥0,即a≥-1时,f(a+1)=(a+1)(a-3);
当a+1<0,即a<-1时,f(a+1)=(a+1)(a+5).
点评:该题考查分段函数的性质、一元二次不等式的求解、函数求值等知识,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
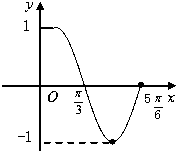 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤ 如图,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB上一点.
如图,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB上一点. 如图,A(1,0),B(
如图,A(1,0),B(