题目内容

A，B为一个钝角三角形的两个锐角，下列关系式中正确的是
 
．（写出所有符合要求的题号）
①sinA+cosA=0.99  
②（sinA-cosA）（sinA+cosA）=
2
  
③tanAtanB＜1 
④sinA+sinB＜
2
  
⑤cosA+cosB＞1 
⑥
1
2
tan（A+B）＜tan
A+B
2
．
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：利用同角三角函数基本关系式对①②③④⑤⑥六个选项逐一判断即可．
解答： 解：①sinA+cosA=
2
sin（A+
π
4
），
∵0＜A＜
π
2
，即
π
4
＜A+
π
4
＜
3π
4
，
∴
2
2
＜sin（A+
π
4
）＜1，即1＜
2
sin（A+
π
4
）＜
2
，
则sinA+cosA≠0.99，本选项错误；
②（sinA-cosA）（sinA+cosA）=sin2A-cos2A=-cos2A，
∵-1≤-cos2A≤1，
∴-cos2A≠
2
，本选项错误；
③若tanAtanB=
sinAsinB
cosAcosB
＜1，则有cosAcosB-sinAsinB=cos（A+B）=-cosC＞0，即cosC＜0，C为钝角，显然正确；
④依题意，A+B＜
π
2
，sinB＜sin（
π
2
-A）=cosA，
故sinA+sinB＜sinA+cosA=
2
sin（A+
π
4
）＜
2
，本选项正确；
⑤同理可得cosA+cosB＞1，即选项⑤正确；
⑥不妨令A=B=
π
6
，则
1
2
tan（A+B）=
3
2
＞
3
3
=tan
A+B
2
，故选项⑥错误；
综上所述，关系式中正确的是③④⑤，
故答案为：③④⑤．
点评：本题考查同角三角函数基本关系的运用，考查转化思想与运算求解能力，属于中档题．
练习册系列答案
相关题目
化简：
ln22+ln
1
4
+1
．
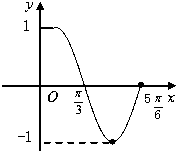如图是函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|≤
π
2
）的部分图象．
（Ⅰ）求函数f（x）的表达式；
（Ⅱ）若函数f（x）满足方程f（x）=a（0＜a＜1），求在[0，2π]内的所有实数根之和；
（Ⅲ）把函数y=f（x）的图象的周期扩大为原来的两倍，然后向右平移
2π
3
个单位，再把纵坐标伸长为原来的两倍，最后向上平移一个单位得到函数y=g（x）的图象．若对任意的0≤m≤3，方程|g（kx）|=m在区间[0，
5π
6
]上至多有一个解，求正数k的取值范围．
如图，A（1，0），B（
2
2
，
2
2
），C（0，1），D（-
2
2
，
2
2
），E（-1，0），F（-
2
2
，-
2
2
），G（0，-1），H（
2
2
，-
2
2
）这8个点中随机取两点与原点O（0，0）构成一个“平面几何体”，记该“平面几何体”的面积为随机变量S（当选取的两点与原点O在同一直线上时，此“平面几何体”的面积S=0）．
（1）求S=0的概率；
（2）求S的分布列与数学期望ES．
已知等差数列{an}的前n项和为Sn，且满足：a3=6，a5+a7=24．
（1）求an和Sn；
（2）设bn=（
2
） an，求数列{bn}的前项和Tn．
已知A（1，0，0），B（0，1，1），C（1，1，0），D（1，2，0），E（0，0，1），则直线DE与平面ABC的位置关系是
 
．
已知数列{an}满足：a1=2，an+1=an2-nan+1，令bn=
1
a n•a n+1
，则数列{bn}的前n项和Sn=
．
若函数f（x）=x+|x-a|的最小值为3a+2，则实数a的值为
 
．
已知离心率为
6
2
的双曲线C：
x2
a2
-
y2
3
=1（a＞0）的左焦点与抛物线y2=2mx的焦点重合，则实数m=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网