题目内容
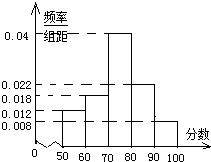 某次素质测试,随机抽取了部分学生的成绩,得到如图所示的频率分布直方图.
某次素质测试,随机抽取了部分学生的成绩,得到如图所示的频率分布直方图.(1)估计成绩的平均值;
(2)若成绩排名前5的学生中,有一人是学生会主席,从这5人中推荐3人参加自主招生考试,试求这3人中含该学生会主席的概率.
考点:古典概型及其概率计算公式,频率分布直方图,众数、中位数、平均数
专题:概率与统计
分析:(1)求每个小矩形底边中点的横坐标乘以对应小矩形的面积之和,可得数据的平均数;
(2)计算从综合素质成绩排名前5名中任选3人的选法种数和3人中含该学生会主席的选法种数,利用古典概型概率公式计算.
(2)计算从综合素质成绩排名前5名中任选3人的选法种数和3人中含该学生会主席的选法种数,利用古典概型概率公式计算.
解答:
解:(1)组距为10,各组的频率分别为0.12,0.18,0.4,0.22,0.08.
分数的平均值
=55×0.12+65×0.18+75×0.4+85×0.22+95×0.08=6.6+11.7+30+18.7+7.6=74.6,
∴学生综合素质成绩的平均值为74.6;
(2)记学生会主席为A,其余四人为1,2,3,4.五人中任推三人,基本事件为:
(A,1,2)(A,1,3)(A,1,4)(A,2,3)(A,2,4)(A,3,4)
(1,2,3)(1,2,4)(1,3,4)(2,3,4)共10个.
满足要求的有6个,记所求事件为M,P(M)=
=
.
分数的平均值
. |
| x |
∴学生综合素质成绩的平均值为74.6;
(2)记学生会主席为A,其余四人为1,2,3,4.五人中任推三人,基本事件为:
(A,1,2)(A,1,3)(A,1,4)(A,2,3)(A,2,4)(A,3,4)
(1,2,3)(1,2,4)(1,3,4)(2,3,4)共10个.
满足要求的有6个,记所求事件为M,P(M)=
| 6 |
| 10 |
| 3 |
| 5 |
点评:本题考查了频率分布直方图,考查了古典概型的概率计算,解题的关键是求得符合条件的基本事件个数.

练习册系列答案
相关题目
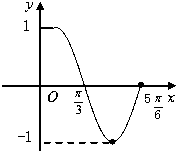 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤ 如图,A(1,0),B(
如图,A(1,0),B(