题目内容
已知f(x)=a2-a-x,(a>0且a≠1),当x∈[1,2]时函数f(x)的最大值为
,求此时a的值.
| 3 |
| 2 |
考点:函数的最值及其几何意义
专题:计算题,函数的性质及应用
分析:对a的取值进行讨论,运用指数函数的单调性进行求解.
解答:
解:①当a>1时,0<a-1<1,
f(x)=a2-a-x单调递增,则x=2时f(x)=
,
∴a2-a-2=
,∴a=
或a=-
(舍去)
②当0<a<1时,a-1>1,
f(x)=a2-a-x单调递减,则x=1时f(x)=
,无解.
综上,a=
f(x)=a2-a-x单调递增,则x=2时f(x)=
| 3 |
| 2 |
∴a2-a-2=
| 3 |
| 2 |
| 2 |
| 2 |
②当0<a<1时,a-1>1,
f(x)=a2-a-x单调递减,则x=1时f(x)=
| 3 |
| 2 |
综上,a=
| 2 |
点评:本题考查了指数函数的单调性,考查学生的计算能力,属于中档题.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
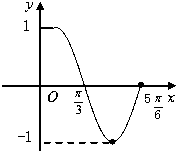 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤ 如图,A(1,0),B(
如图,A(1,0),B(