题目内容
3.若正四棱锥的底面边长为2(单位:cm),侧面积为8(单位:cm2),则它的体积为$\frac{4\sqrt{3}}{3}$(单位:cm3).分析 根据侧面积计算出棱锥的斜高,利用勾股定理计算棱锥的高.
解答 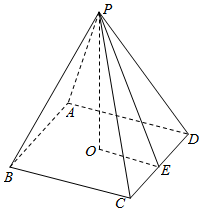 解:设四棱锥为P-ABCD,底面ABCD的中心为O取CD中点E,连结PE,OE.
解:设四棱锥为P-ABCD,底面ABCD的中心为O取CD中点E,连结PE,OE.
则PE⊥CD.OE=$\frac{1}{2}BC$=1.
∵S侧面=4S△PCD=4×$\frac{1}{2}$×CD×PE=8,∴PE=2.
∴PO=$\sqrt{3}$,
∴正四棱锥体积V=$\frac{1}{3}×{2}^{2}×\sqrt{3}$=$\frac{4\sqrt{3}}{3}$.
故答案为$\frac{4\sqrt{3}}{3}$.
点评 本题考查了棱锥的结构特征,体积计算,属于基础题.

练习册系列答案
相关题目
13.已知a=0.993,b=log20.6,c=log3π,则( )
| A. | c<a<b | B. | b<c<a | C. | a<b<c | D. | b<a<c |
11.已知点P(a,b)关于直线l的对称点为Q(3-b,3-a),则直线l的方程是( )
| A. | x+y-3=0 | B. | x+y+b-a=0 | C. | x+y-a-b=0 | D. | x-y+3=0 |
15.直线m,n满足m?α,n?α,则n⊥m是n⊥α( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
12.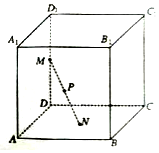 如图,已知正方体ABCD-A1B1C1D1的棱长为1,长为1的线段MN的一个端点M在棱DD1上运动,点N在正方形ABCD内运动,则MN中点P的轨迹的面积为( )
如图,已知正方体ABCD-A1B1C1D1的棱长为1,长为1的线段MN的一个端点M在棱DD1上运动,点N在正方形ABCD内运动,则MN中点P的轨迹的面积为( )
 如图,已知正方体ABCD-A1B1C1D1的棱长为1,长为1的线段MN的一个端点M在棱DD1上运动,点N在正方形ABCD内运动,则MN中点P的轨迹的面积为( )
如图,已知正方体ABCD-A1B1C1D1的棱长为1,长为1的线段MN的一个端点M在棱DD1上运动,点N在正方形ABCD内运动,则MN中点P的轨迹的面积为( )| A. | $\frac{π}{2}$ | B. | $\frac{π}{16}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{4}$ |
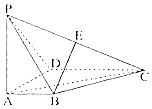 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=1,$AB=\frac{1}{2}$,点E为棱PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=1,$AB=\frac{1}{2}$,点E为棱PC的中点.