题目内容
12.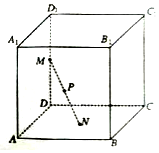 如图,已知正方体ABCD-A1B1C1D1的棱长为1,长为1的线段MN的一个端点M在棱DD1上运动,点N在正方形ABCD内运动,则MN中点P的轨迹的面积为( )
如图,已知正方体ABCD-A1B1C1D1的棱长为1,长为1的线段MN的一个端点M在棱DD1上运动,点N在正方形ABCD内运动,则MN中点P的轨迹的面积为( )| A. | $\frac{π}{2}$ | B. | $\frac{π}{16}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{4}$ |
分析 根据题意,连接N点与D点,得到一个直角三角形△NMD,P为斜边MN的中点,所以|PD|的长度不变,进而得到点P的轨迹是球面的一部分.
解答  解:如图可得,端点N在正方形ABCD内运动,连接N点与D点,
解:如图可得,端点N在正方形ABCD内运动,连接N点与D点,
由ND,DM,MN构成一个直角三角形,
设P为MN的中点,根据直角三角形斜边上的中线长度为斜边的一半可得:
不论△MDN如何变化,P点到D点的距离始终等于$\frac{1}{2}$.
故P点的轨迹是一个以D为中心,半径为$\frac{1}{2}$的球的$\frac{1}{8}$球面.
所以MN中点P的轨迹的面积为$\frac{π}{8}$,
故选:C.
点评 解决此类问题的关键是熟悉结合体的结构特征与球的定义以及其表面积的计算公式.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
20.方程$|x|-2=\sqrt{4-{{({y-2})}^2}}$表示的曲线是( )
| A. | 一个圆 | B. | 半圆 | C. | 两个圆 | D. | 两个半圆 |
17.设△ABC的内角A,B,C所对的边长分别为a,b,c,若bcosC+ccosB=2acosA,则A=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$或$\frac{2π}{3}$ |
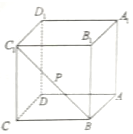 如图,点P是正方体ABCD-A1B1C1D1的面对角线BC1(线段BC1)上运动,给出下列五个命题:
如图,点P是正方体ABCD-A1B1C1D1的面对角线BC1(线段BC1)上运动,给出下列五个命题: