题目内容
2.定义“函数y=f(x)是D上的a级类周期函数”如下:函数y=f(x),x∈D,对于给定的非零常数a,总存在非零常数T,使得定义域D内的任意实数x都有af(x)=f(x+T)恒成立,此时T为f(x)的周期.若y=f(x)是[1,+∞)上的a级类周期函数,且T=1,当x∈[1,2)时,f(x)=2x(2x+1),且y=f(x)是[1,+∞)上的单调递增函数,则实数a的取值范围为( )| A. | $[{\frac{5}{6},+∞})$ | B. | [2,+∞) | C. | $[{\frac{10}{3},+∞})$ | D. | [10,+∞) |
分析 分类讨论f得出f(x)在[1,+∞)上单调递增,
得出an•2n-n(2n-2n+3)≥an-1•2n-(n-1)(2n-2n+5),
解得a的取值范围.
解答 解:∵x∈[1,2)时,f(x)=2x(2x+1),
∴当x∈[2,3)时,f(x)=af(x-1)=a•2x-1(2x-1);
当x∈[n,n+1)时,f(x)=an-1f[x-(n-1)]=an-1•2x-n+1(2x-2n+3);
即x∈[n,n+1)时,f(x)=an-1•2x-n+1(2x-2n+3),n∈N*,
∵f(x)在[1,+∞)上单调递增,
∴a>0且an•2n-n(2n-2n+3)≥an-1•2n-(n-1)(2n-2n+5),
解得a≥$\frac{10}{3}$,
∴实数a的取值范围是[$\frac{10}{3}$,+∞).
故选:C.
点评 本题综合考查了函数的性质与分类讨论思想的应用问题,是难题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
2.已知长方体切去一个角的几何体直观图如图1所示给出下列4个平面图如图2:
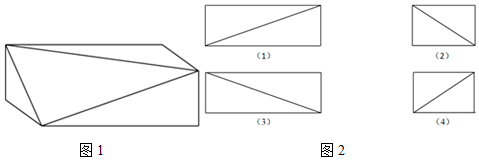
则该几何体的主视图、俯视图、左视图的序号依次是( )

则该几何体的主视图、俯视图、左视图的序号依次是( )
| A. | (1)(3)(4) | B. | (2)(4)(3) | C. | (1)(3)(2) | D. | (2)(4)(1) |
13.已知直线x=$\frac{b}{2}$与椭圆C:$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}=1$(a>b>0)交于A、B两点,若椭圆C的两个焦点与A、B两点可以构成一个矩形,则椭圆C的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{10}}{4}$ |
10.已知函数f(x)=xlnx+x(x-a)2(a∈R),若存在$x∈[{\frac{1}{2},2}]$,使得f(x)>xf'(x)成立,则实数a的取值范围是( )
| A. | $({\frac{9}{4},+∞})$ | B. | $({\frac{3}{2},+∞})$ | C. | $({\sqrt{2},+∞})$ | D. | (3,+∞) |
17.为便民惠民,某通信运营商推出“优惠卡活动”.其内容如下:卡号的前7位是固定的,后四位从“0000”到“9999”共10000个号码参与该活动,凡卡号后四位带有“6”或“8”的一律作为优惠卡,则“优惠卡”的个数是( )
| A. | 1980 | B. | 4096 | C. | 5904 | D. | 8020 |
14.设倾斜角为α的直线l经过抛物线C:y2=2px(p>0)的焦点F,与抛物线C交于A,B两点,设点A在x轴上方,点B在x轴下方.若$\frac{|AF|}{|BF|}=m$,则cosα的值为( )
| A. | $\frac{m-1}{m+1}$ | B. | $\frac{m}{m+1}$ | C. | $\frac{m-1}{m}$ | D. | $\frac{{2\sqrt{m}}}{m+1}$ |