题目内容

7．在${（2x+\frac{a}{x^2}）^5}$的展开式中x-4的系数为320，则实数a=2．

分析 根据二项式展开式的通项公式，令x的指数等于-4求出r的值，
再利用x-4系数列方程求出a的值．

解答 解：${（2x+\frac{a}{x^2}）^5}$的展开式中，项公式为
Tr+1=${C}_{5}^{r}$•（2x）5-r•${（\frac{a}{{x}^{2}}）}^{r}$=${C}_{5}^{r}$•25-r•ar•x5-3r；
令5-3r=-4，解得r=3；
所以展开式中x-4的系数为
${C}_{5}^{3}$•22•a3=320，
解得a=2．
故答案为：2．

点评 本题考查了利用二项式展开式的通项公式求特定项系数的应用问题，是基础题．

练习册系列答案
相关题目
7．在直角坐标系中，以原点O为极点，x轴的正半轴为极轴建立极坐标系，点A的极坐标为（4，$\frac{π}{3}$），点B的极坐标为（2$\sqrt{2}$，$\frac{π}{4}$），曲线C的直角坐标方程为：x2+（y-1）2=1．
（Ⅰ）求曲线C和直线AB的极坐标方程；
（Ⅱ）过点O的射线l交曲线C于M点，交直线AB于N点，若|OM|•|ON|=4，求射线l所在直线的直角坐标方程．
18．已知数列{an}，a1=2，an=$\frac{1}{n}$+（1-$\frac{1}{n}$）an-1（n≥2，n∈N*）．
（1）证明：数列{nan}是等差数列；
（2）记bn=$\frac{1}{{n}^{2}{a}_{n}}$，{bn}的前n项和Sn，求证Sn＜1．
15．观察以下三个不等式：
①（12+22+32）（32+42+52）≥（1×3+2×4+3×5）2；
②（72+92+102）（62+82+112）≥（7×6+9×8+10×11）2；
③（202+302+20172）（992+902+20162）≥（20×99+30×90+2017×2016）2；
若2x+y+z=-7，x，y，z∈R时，则（x+1）2+（y+2）2+（z+1）2的最小值为$\frac{2}{3}$．
2．定义“函数y=f（x）是D上的a级类周期函数”如下：函数y=f（x），x∈D，对于给定的非零常数a，总存在非零常数T，使得定义域D内的任意实数x都有af（x）=f（x+T）恒成立，此时T为f（x）的周期．若y=f（x）是[1，+∞）上的a级类周期函数，且T=1，当x∈[1，2）时，f（x）=2x（2x+1），且y=f（x）是[1，+∞）上的单调递增函数，则实数a的取值范围为（　　）
A．$[{\frac{5}{6}，+∞}）$B．[2，+∞）C．$[{\frac{10}{3}，+∞}）$D．[10，+∞）
12．已知曲线$f（x）=\frac{{{{ln}^2}x+alnx+a}}{x}$在点（e，f（e））处的切线与直线2x+e2y=0平行，a∈R．
（1）求a的值；
（2）求证：$\frac{f（x）}{x}＞\frac{a}{e^x}$．
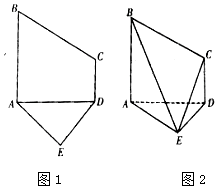19．已知五边形ABCDE是由直角梯形ABCD和等腰直角三角形ADE构成，如图所示，AB⊥AD，AE⊥DE，AB∥CD，且AB=2CD=2DE=4，将五边形ABCDE沿着AD折起，且使平面ABCD⊥平面ADE．
（Ⅰ）若M为DE中点，边BC上是否存在一点N，使得MN∥平面ABE？若存在，求$\frac{BN}{BC}$的值；若不存在，说明理由；
（Ⅱ）求四面体B-CDE的体积．
16．某校在高二年级开展了体育分项教学活动，将体育课分为大球（包括篮球、排球、足球）、小球（包括乒乓球、羽毛球）、田径、体操四大项（以下简称四大项，并且按照这个顺序）．为体现公平，学校规定时间让学生在电脑上选课，据初步统计，在全年级980名同学中，有意申报四大项的人数之比为3：2：1：1，而实际上由于受多方面条件影响，最终确定的四大项人数必须控制在2：1：3：1，选课不成功的同学由电脑自动调剂到田径类．
（Ⅰ）随机抽取一名同学，求该同学选课成功（未被调剂）的概率；
（Ⅱ）某小组有五名同学，有意申报四大项的人数分别为2、1、1、1，记最终确定到田径类的人数为X，求X的分布列及数学期望EX．
17．已知集合A={x|x＞0}，B={x|x2-2x-3＜0}，则A∩B=（　　）
A．（-1，0）B．（0，3）C．（-∞，0）∪（3，+∞）D．（-1，3）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网