题目内容
10．已知函数f（x）=xlnx+x（x-a）2（a∈R），若存在$x∈[{\frac{1}{2}，2}]$，使得f（x）＞xf'（x）成立，则实数a的取值范围是（ ）| A． | $（{\frac{9}{4}，+∞}）$ | B． | $（{\frac{3}{2}，+∞}）$ | C． | $（{\sqrt{2}，+∞}）$ | D． | （3，+∞） |
分析 由f（x）＞xf'（x）成立，可得[$\frac{f（x）}{x}$]′＜0，设g（x）=$\frac{f（x）}{x}$=lnx+（x-a）2，
则存在$x∈[{\frac{1}{2}，2}]$，使得g′（x）=$\frac{1}{x}$+2（x-a）＜0成立，a＞（x+$\frac{1}{2x}$）min．
解答 解：由f（x）＞xf'（x）成立，可得[$\frac{f（x）}{x}$′＜0，设g（x）=$\frac{f（x）}{x}$=lnx+（x-a）2，
则存在$x∈[{\frac{1}{2}，2}]$，使得g′（x）＜0成立，即g′（x）=$\frac{1}{x}$+2（x-a）＜0成立，即a＞x+$\frac{1}{2x}$成立．
a＞（x+$\frac{1}{2x}$）min．又x+$\frac{1}{2x}$≥2$\sqrt{x•\frac{1}{2x}}$=$\sqrt{2}$，∴$a＞\sqrt{2}$．当且仅当x=$\frac{\sqrt{2}}{2}$时取等号．
故选：C
点评 本题考查了导数的应用，分离参数法求参数范围，属于中档题．
练习册系列答案
相关题目
2．定义“函数y=f（x）是D上的a级类周期函数”如下：函数y=f（x），x∈D，对于给定的非零常数a，总存在非零常数T，使得定义域D内的任意实数x都有af（x）=f（x+T）恒成立，此时T为f（x）的周期．若y=f（x）是[1，+∞）上的a级类周期函数，且T=1，当x∈[1，2）时，f（x）=2x（2x+1），且y=f（x）是[1，+∞）上的单调递增函数，则实数a的取值范围为（ ）
| A． | $[{\frac{5}{6}，+∞}）$ | B． | [2，+∞） | C． | $[{\frac{10}{3}，+∞}）$ | D． | [10，+∞） |
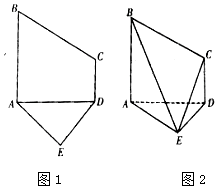已知五边形ABCDE是由直角梯形ABCD和等腰直角三角形ADE构成，如图所示，AB⊥AD，AE⊥DE，AB∥CD，且AB=2CD=2DE=4，将五边形ABCDE沿着AD折起，且使平面ABCD⊥平面ADE．