题目内容
11.等比数列{an}中,a1+a4+a7=2,a3+a6+a9=18,则{an}的前9项和S9=14或26.分析 由题意列式求得公比,然后分类求出a2+a5+a8,作和得答案.
解答 解:在等比数列{an}中,由a1+a4+a7=2,a3+a6+a9=18,得
${q}^{2}=\frac{{a}_{3}+{a}_{6}+{a}_{9}}{{a}_{1}+{a}_{4}+{a}_{7}}=\frac{18}{2}=9$,∴q=±3.
当q=-3时,a2+a5+a8=-6,S9=a1+a2+…+a9=2-6+18=14;
当q=3时,a2+a5+a8=6,S9=a1+a2+…+a9=2+6+18=26.
故答案为:14或26.
点评 本题考查等比数列的性质,考查了等比数列的前n项和,是基础的计算题.

练习册系列答案
相关题目
2.定义“函数y=f(x)是D上的a级类周期函数”如下:函数y=f(x),x∈D,对于给定的非零常数a,总存在非零常数T,使得定义域D内的任意实数x都有af(x)=f(x+T)恒成立,此时T为f(x)的周期.若y=f(x)是[1,+∞)上的a级类周期函数,且T=1,当x∈[1,2)时,f(x)=2x(2x+1),且y=f(x)是[1,+∞)上的单调递增函数,则实数a的取值范围为( )
| A. | $[{\frac{5}{6},+∞})$ | B. | [2,+∞) | C. | $[{\frac{10}{3},+∞})$ | D. | [10,+∞) |
6.已知函数f(x)=$\sqrt{3}$sin(2x-φ)-cos(2x-φ)(|φ|<$\frac{π}{2}$)的图象关于y轴对称,则f(x)在区间$[{-\frac{π}{6},\frac{π}{3}}]$上的最大值为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2 |
3.随着手机的发展,“微信”逐渐成为人们交流的一种形式,某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频率分布及“使用微信交流”赞成人数如下表.
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面2×2列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
(2)若从年龄在[55,65)的被调查人中随机选取2人进行追踪调查,求2人中至少有1人不赞成“使用微信交流”的概率.
参考数据:
(K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 赞成 | |||
| 不赞成 | |||
| 合计 |
参考数据:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
1.已知f(x)=$\frac{e^x}{{{x^2}+a}}({a>0})$的两个极值点分别为x1,x2(x1<x2),则a(lnx1+lnx2)的取值范围是( )
| A. | $[{-\frac{1}{e},0})$ | B. | (0,+∞) | C. | (0,1) | D. | $[{-\frac{1}{e},+∞})$ |
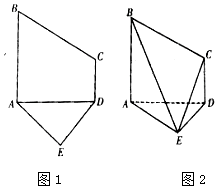 已知五边形ABCDE是由直角梯形ABCD和等腰直角三角形ADE构成,如图所示,AB⊥AD,AE⊥DE,AB∥CD,且AB=2CD=2DE=4,将五边形ABCDE沿着AD折起,且使平面ABCD⊥平面ADE.
已知五边形ABCDE是由直角梯形ABCD和等腰直角三角形ADE构成,如图所示,AB⊥AD,AE⊥DE,AB∥CD,且AB=2CD=2DE=4,将五边形ABCDE沿着AD折起,且使平面ABCD⊥平面ADE.