题目内容
12．函数f（x）=xex+1的图象在点（0，f（0））处的切线方程是x-y+1=0．分析 求出函数的导数，可得切线的斜率，求出切点，运用斜截式方程，即可得到所求切线的方程．
解答 解：f（x）=xex+1的导数为f′（x）=（x+1）ex，
可得在点（0，f（0））处的切线斜率为k=1，
又切点为（0，1），
则在点（0，f（0））处的切线方程为y=x+1．
即为x-y+1=0．
故答案为：x-y+1=0．
点评 本题考查导数的运用：求切线的方程，考查导数的几何意义，正确求导和运用斜截式方程是解题的关键，考查运算能力，属于基础题．
练习册系列答案
相关题目
2．定义“函数y=f（x）是D上的a级类周期函数”如下：函数y=f（x），x∈D，对于给定的非零常数a，总存在非零常数T，使得定义域D内的任意实数x都有af（x）=f（x+T）恒成立，此时T为f（x）的周期．若y=f（x）是[1，+∞）上的a级类周期函数，且T=1，当x∈[1，2）时，f（x）=2x（2x+1），且y=f（x）是[1，+∞）上的单调递增函数，则实数a的取值范围为（ ）
| A． | $[{\frac{5}{6}，+∞}）$ | B． | [2，+∞） | C． | $[{\frac{10}{3}，+∞}）$ | D． | [10，+∞） |
3．随着手机的发展，“微信”逐渐成为人们交流的一种形式，某机构对“使用微信交流”的态度进行调查，随机抽取了50人，他们年龄的频率分布及“使用微信交流”赞成人数如下表．
（1）若以“年龄45岁为分界点”，由以上统计数据完成下面2×2列联表，并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关；
（2）若从年龄在[55，65）的被调查人中随机选取2人进行追踪调查，求2人中至少有1人不赞成“使用微信交流”的概率．
参考数据：
（K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
| 年龄（岁） | [15，25） | [25，35） | [35，45） | [45，55） | [55，65） | [65，75） |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 赞成 | |||
| 不赞成 | |||
| 合计 |
参考数据：
| P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
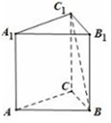
7．如图，在棱长均相等的正三棱柱ABC-A1B1C1中，异面直线AA1与BC1的夹角为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
17．已知集合A={x|x＞0}，B={x|x2-2x-3＜0}，则A∩B=（ ）
| A． | （-1，0） | B． | （0，3） | C． | （-∞，0）∪（3，+∞） | D． | （-1，3） |
1．已知f（x）=$\frac{e^x}{{{x^2}+a}}（{a＞0}）$的两个极值点分别为x1，x2（x1＜x2），则a（lnx1+lnx2）的取值范围是（ ）
| A． | $[{-\frac{1}{e}，0}）$ | B． | （0，+∞） | C． | （0，1） | D． | $[{-\frac{1}{e}，+∞}）$ |
2．已知函数y=sin（πx+φ）-2cos（πx+φ）（0＜φ＜π）的图象关于点（1，0）对称，则tanφ=（ ）
| A． | -$\frac{1}{2}$ | B． | -2 | C． | $\frac{1}{2}$ | D． | 2 |