题目内容
函数y=mx2-4mx-m2+2m+3，当x∈[-1，3]时有最大值3，则m的值为 ．
考点：二次函数的性质
专题：函数的性质及应用
分析：求出：对称轴x=2，x∈[-1，3]，分类讨论求解即可①当m＞0时，f（-1）=3，②当m＜0时，f（2）=3，③当m=0时，f（x）=3，
解答：
解：①当m=0时，f（x）=3，
∴x∈[-1，3]时有最大值3，
当m≠0时，函数y=mx2-4mx-m2+2m+3的对称轴x=2，x∈[-1，3]
②当m＞0时，f（-1）=3，
-m2+7m+3=3，
解得m=7或m=0（舍去），
③当m＜0时，f（2）=3，
即-m2-2m+3=3，
解得m=0（舍去），m=-2，
综上；m=-2，或m=7，m=0
故答案为：-2，0，7
∴x∈[-1，3]时有最大值3，
当m≠0时，函数y=mx2-4mx-m2+2m+3的对称轴x=2，x∈[-1，3]
②当m＞0时，f（-1）=3，
-m2+7m+3=3，
解得m=7或m=0（舍去），
③当m＜0时，f（2）=3，
即-m2-2m+3=3，
解得m=0（舍去），m=-2，
综上；m=-2，或m=7，m=0
故答案为：-2，0，7
点评：本题考查了函数的性质，分类讨论求解最大值，关键是取舍变量的值，属于中档题．
练习册系列答案
相关题目
已知双曲线
-
=1（a＞0，b＞0）的离心率为
，则椭圆
+
=1的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
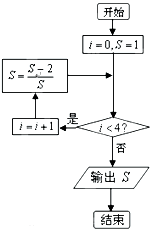
执行如图所示的程序框图，输出的S值为 （ ）
| A、-1 | ||
| B、3 | ||
C、
| ||
| D、-5 |
若曲线y=x2+ax+b在点（0，b）处的切线方程是y=x+1，则（ ）
| A、a=1，b=1 |
| B、a=-1，b=1 |
| C、a=1，b=-1 |
| D、a=-1，b=-1 |