题目内容
若曲线y=x2+ax+b在点(0,b)处的切线方程是y=x+1,则( )
| A、a=1,b=1 |
| B、a=-1,b=1 |
| C、a=1,b=-1 |
| D、a=-1,b=-1 |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:曲线y=x2+ax+b在点(0,b)处的切线方程是y=x+1可知点在直线上,且导数与斜率相等,从而解得.
解答:
解:y′=2x+a;
∵曲线y=x2+ax+b在点(0,b)处的切线方程是y=x+1,
∴
;
解得,a=1,b=1;
故选A.
∵曲线y=x2+ax+b在点(0,b)处的切线方程是y=x+1,
∴
|
解得,a=1,b=1;
故选A.
点评:本题考查了导数的求法与其几何意义的应用,属于基础题.

练习册系列答案
相关题目
一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如右图).为了分析居民的收入与年龄、学历、职业等方面的关系,每隔500元一段要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000)(元)月收入段应抽出的人数为( )
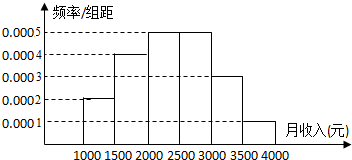

| A、20 | B、25 | C、35 | D、45 |
在平面直角坐标系中,曲线经过旋转或平移所产生的新双曲线与原双曲线具有相同的离心率和焦距,称它们为一组“任性双曲线”;例如将等轴双曲线x2-y2=2绕原点逆时针转动45°,就会得到它的一条“任性双曲线”y=
;根据以上材料可推理得出双曲线y=
的焦距为( )
| 1 |
| x |
| 3x+1 |
| x-1 |
| A、4 | ||
B、4
| ||
| C、8 | ||
D、8
|
设定点F1(0,-3)、F2(0,3)动点P满足条件|PF1|-a=
-|PF2|(a>0)则点P的轨迹是( )
| 9 |
| a |
| A、椭圆 | B、线段 |
| C、不存在 | D、椭圆或线段 |