题目内容
已知各项都是正数的等比数列{an}满足a7=a6+2a5,若存在不同的两项am和an,使得am•an=16a12,则
+
的最小值是 .
| 1 |
| m |
| 4 |
| n |
考点:基本不等式在最值问题中的应用,等比数列的性质
专题:综合题,不等式的解法及应用
分析:由a7=a6+2a5 求得q=2,代入am•an=16a12求得m+n=6,利用基本不等式求出它的最小值.
解答:
解:由各项均为正数的等比数列{an}满足a7=a6+2a5,可得q2-q-2=0,∴q=2.
∵am•an=16a12,∴qm+n-2=16,∴2m+n-2=24,∴m+n=6,
∴
+
=
(m+n)(
+
)=
(5+
+
)≥
(5+4)=
,
当且仅当
=
时,等号成立.
故
+
的最小值等于
,
故答案为:
.
∵am•an=16a12,∴qm+n-2=16,∴2m+n-2=24,∴m+n=6,
∴
| 1 |
| m |
| 4 |
| n |
| 1 |
| 6 |
| 1 |
| m |
| 4 |
| n |
| 1 |
| 6 |
| n |
| m |
| 4m |
| n |
| 1 |
| 6 |
| 3 |
| 2 |
当且仅当
| n |
| m |
| 4m |
| n |
故
| 1 |
| m |
| 4 |
| n |
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本题主要考查等比数列的通项公式,基本不等式的应用,属于基础题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
设定点F1(0,-3)、F2(0,3)动点P满足条件|PF1|-a=
-|PF2|(a>0)则点P的轨迹是( )
| 9 |
| a |
| A、椭圆 | B、线段 |
| C、不存在 | D、椭圆或线段 |
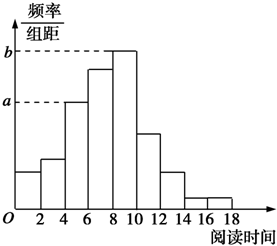 从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频率分布表和频率分布直方图:
从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频率分布表和频率分布直方图: