题目内容
已知p:不等式x2-2x-m>0解集为R,q:集合A={x|x2+2x-m-1=0,x∈R},且A≠∅.且p∧q为真,求实数m的取值范围.
考点:复合命题的真假
专题:简易逻辑
分析:根据一元二次不等式的解及一元二次方程的解和判别式的关系,求出p,q下的m的取值,根据p∧q为真知p,q都为真,这样求p,q下m取值范围的交集即可.
解答:
解:p:不等式x2-2x-m>0解集为R;
则△=4+4m<0,∴m<-1;
q:集合A={x|x2+2x-m-1=0,x∈R},且A≠∅;
即方程x2+2x-m-1=0有实根;
∴△=4+4(m+1)≥0,m≥-2;
又p∧q为真,故p、q均为真;
∴m<-1且m≥-2,∴-2≤m<-1;
∴实数m的取值范围是[-2,-1).
则△=4+4m<0,∴m<-1;
q:集合A={x|x2+2x-m-1=0,x∈R},且A≠∅;
即方程x2+2x-m-1=0有实根;
∴△=4+4(m+1)≥0,m≥-2;
又p∧q为真,故p、q均为真;
∴m<-1且m≥-2,∴-2≤m<-1;
∴实数m的取值范围是[-2,-1).
点评:考查一元二次不等式的解、一元二次方程的解和判别式△的关系,p∧q的真假和p,q真假的关系.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
给出四个命题:
(1)若sin2A=sin2B,则△ABC为等腰三角形;
(2)若sinA=cosB,则△ABC为直角三角形;
(3)若cos(A-B)cos(B-C)cos(C-A)=1,则△ABC为正三角形.
以上正确命题的个数是( )
(1)若sin2A=sin2B,则△ABC为等腰三角形;
(2)若sinA=cosB,则△ABC为直角三角形;
(3)若cos(A-B)cos(B-C)cos(C-A)=1,则△ABC为正三角形.
以上正确命题的个数是( )
| A、0 | B、1 | C、2 | D、3 |
己知a∈R,则“a=±1”是“a2-1+(a-1)i为纯虚数”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
给出下列图象,其中可能为函数f(x)=x4+ax3+cx+d(a,b,c,d∈R)的图象是( )
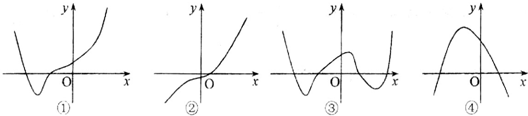

| A、①③ | B、①② | C、③④ | D、②④ |
 如图,电键A、B、C、D闭合的概率分别为p1、p2、p3、p4,且彼此独立,求灯泡亮的概率.
如图,电键A、B、C、D闭合的概率分别为p1、p2、p3、p4,且彼此独立,求灯泡亮的概率.