题目内容

给出下列图象，其中可能为函数f（x）=x4+ax3+cx+d（a，b，c，d∈R）的图象是（　　）
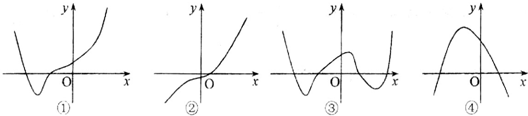
A、①③B、①②C、③④D、②④
考点：函数的图象
专题：函数的性质及应用
分析：先求函数的导函数，由导函数所对应方程的根的情况进行讨论，从而得出原函数的极值情况，再对图象进行筛选．
解答： 解：∵f（x）=x4+ax3+bx2+cx+d（a，b，c，d∈R），
∴f′（x）=4x3+3ax2+2bx+c，
此函数相应方程的根可能有三个或两个或一个，下面分三种情况讨论：
①若方程可能的根有一个，如a，b，c都为0时，f′（x）=0的根只有一个，故函数值先负后正，故函数的图象是先减后增，符合条件的只有①．
②若方程可能的根有两个，函数有两个极值点，函数图象必是先减后增再减型，与题意不符，
③若方程的根有三个，则函数有三个极值点，函数的单调性是先减后增再减再增型，考察②③④得③符合条件
综上讨论知，①③中的图象可能是函数的图象，
故答案为①③，
故选：A
点评：利用导数进行研究函数时，主要的方法是通过研究导函数的零点来与原函数的极值情况结合，从而更易得到函数的单调情况．
练习册系列答案
相关题目
下列判断中所有正确命题的序号是
 
．
①当a=4，b=5，A=30°时，三角形有两解；
②当a=5，b=4，A=60°时，三角形有两解；
③当a=
3
，b=
2
，B=120°时，三角形有一解；
④当a=
3
2
2
，b=
6
，A=60°时，三角形有一解．
已知p：不等式x2-2x-m＞0解集为R，q：集合A={x|x2+2x-m-1=0，x∈R}，且A≠∅．且p∧q为真，求实数m的取值范围．
某工厂某种产品的产量y（千件）与单位成本x（元）之间的关系满足y=60-2.5x，则以下说法正确的是（　　）
A、产品每增加1 000 件，单位成本下降2.5万元
B、产品每减少1 000 件，单位成本上升2.5万元
C、产品每增加1 000 件，单位成本上升2.5万元
D、产品每减少1 000 件，单位成本下降2.5万元
已知函数f（x）=
1
3
x3+2x2+ax+b，g（x）=ex（cx+d），且函数f（x）的导函数为f′（x），若曲线f（x）和g（x）都过点A（0，2），且在点A 处有相同的切线y=4x+2．
（Ⅰ）求a，b，c，d的值；
（Ⅱ）若x≥-2时，mg（x）≥f′（x）-2恒成立，求实数m的取值范围．
已知函数g（x）=1-2x，f[g（x）]=
1-x2
x2
，则f（
1
2
）等于
 
．
?x∈[-1，1]使关于x的不等式x2-2m-5＞0能成立，则m取值范围是
 
．
定义在R上的函数f（x），若对任意x1≠x2，都有x1f（x1）+x2f（x2）＞x1f（x2）+x2f（x1），则称f（x）为“Z函数”，给出下列函数：
①y=
1
3
x3-x2+x-2；②y=2x-（sinx+cosx）；③y=ex+1；④f（x）=
ln|x|， x≠0
0， x=0.
其中是“Z函数”的个数为（　　）
A、1B、2C、3D、4
下列函数中既是奇函数，又在（0，+∞）上单调递增的是（　　）
A、y=sinx
B、y=-x2+
1
x
C、y=x3+3x
D、y=e|x|

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网