题目内容
给出四个命题:
(1)若sin2A=sin2B,则△ABC为等腰三角形;
(2)若sinA=cosB,则△ABC为直角三角形;
(3)若cos(A-B)cos(B-C)cos(C-A)=1,则△ABC为正三角形.
以上正确命题的个数是( )
(1)若sin2A=sin2B,则△ABC为等腰三角形;
(2)若sinA=cosB,则△ABC为直角三角形;
(3)若cos(A-B)cos(B-C)cos(C-A)=1,则△ABC为正三角形.
以上正确命题的个数是( )
| A、0 | B、1 | C、2 | D、3 |
考点:命题的真假判断与应用
专题:解三角形,简易逻辑
分析:由sin2A=sin2B,得2A=2B或2A+2B=π,即A=B或C=
,从而说明命题(1)错误;
举例说明命题(2)错误;
直接由已知的等式推出(3)正确.
| π |
| 2 |
举例说明命题(2)错误;
直接由已知的等式推出(3)正确.
解答:
解:(1)若sin2A=sin2B,则 2A=2B,或 2A+2B=π,即A=B 或C=
,
故△ABC为等腰三角形或直角三角形,故①不正确.
(2)若sinB=cosA,例如∠B=100°和∠A=10°,满足sinB=cosA,
则△ABC不是直角三角形,故②不正确.
(3)∵-1≤cos(A-B)≤1,-1≤cos(B-C)≤1,-1≤cos(C-A)≤1,
又cos(A-B)cos(B-C)cos(C-A)=1,
∴cos(A-B)=1,cos(B-C)=1,cos(C-A)=1,
结合A、B、C<180°,可得A-B=B-C=C-A=0,
故△ABC为正三角形.
∴正确的命题是1个.
故选:B.
| π |
| 2 |
故△ABC为等腰三角形或直角三角形,故①不正确.
(2)若sinB=cosA,例如∠B=100°和∠A=10°,满足sinB=cosA,
则△ABC不是直角三角形,故②不正确.
(3)∵-1≤cos(A-B)≤1,-1≤cos(B-C)≤1,-1≤cos(C-A)≤1,
又cos(A-B)cos(B-C)cos(C-A)=1,
∴cos(A-B)=1,cos(B-C)=1,cos(C-A)=1,
结合A、B、C<180°,可得A-B=B-C=C-A=0,
故△ABC为正三角形.
∴正确的命题是1个.
故选:B.
点评:本题考查了命题的真假判断与应用,考查了三角形形状的判断,是中档题.

练习册系列答案
相关题目
若(2-3x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,则|a0|+|a1|+|a2|+|a3|+|a4|+|a5|等于( )
| A、55 |
| B、-1 |
| C、25 |
| D、-25 |
89×90×91×92×…×100可表示为( )
A、A
| ||
B、
| ||
C、
| ||
D、
|


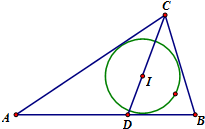 如图,△ABC中,点A(-1,0),B(1,0).圆I是△ABC的内切圆,且CI延长线交AB与点D,若
如图,△ABC中,点A(-1,0),B(1,0).圆I是△ABC的内切圆,且CI延长线交AB与点D,若