题目内容
1.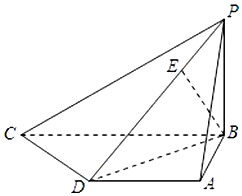 已知四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,AB=AD=1,BC=2,又PB⊥平面ABCD,且PB=1,点E在棱PD上,且BE⊥PD.
已知四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,AB=AD=1,BC=2,又PB⊥平面ABCD,且PB=1,点E在棱PD上,且BE⊥PD.(Ⅰ)求异面直线PA与CD所成的角的大小;
(Ⅱ)求证:BE⊥平面PCD;
(Ⅲ)求二面角A-PD-B的大小.
分析 (Ⅰ)由于直线PA与CD不在同一平面内,要把两条异面直线移到同一平面内,做AF∥CD,异面直线PA与CD所成的角与AF与PA所成的角相等.
(Ⅱ)证明CD⊥平面PDB,可得CD⊥BE,结合BE⊥PD即可得证.
(Ⅲ)连接AF,交BD于点O,则AO⊥BD.过点O作OH⊥PD于点H,连接AH,则AH⊥PD,则∠AHO为二面角A-PD-B的平面角.
解答 (Ⅰ)解:取BC中点F,连接AF,则CF=AD,且CF∥AD,
∴四边形ADCF是平行四边形,
∴AF∥CD,
∴∠PAF(或其补角)为异面直线PA与CD所成的角
∵PB⊥平面ABCD,∴PB⊥BA,PB⊥BF.
∵PB=AB=BF=1,
∴AB⊥BC,
∴PA=PF=AF=$\sqrt{2}$.
∴△PAF是正三角形,∠PAF=60°
即异面直线PA与CD所成的角等于60°.
(Ⅱ)证明:由(Ⅰ)知,CF=BF=DF,∴∠CDB=90°.
∴CD⊥BD
又PB⊥平面PBD,∴PB⊥CD、
∵PB∩BD=B,
∴CD⊥平面PBD,
∴CD⊥BE
∵CD∩PD=D,BE⊥PD
∴BE⊥平面PCD;
(Ⅲ)解:连接AF,交BD于点O,则AO⊥BD、
∵PB⊥平面ABCD,
∴平面PBD⊥平面ABD,
∴AO⊥平面PBD、
过点O作OH⊥PD于点H,连接AH,则AH⊥PD、
∴∠AHO为二面角A-PD-B的平面角.
在Rt△ABD中,AO=$\frac{\sqrt{2}}{2}$.
在Rt△PAD中,AH=$\frac{PA•AD}{PD}$=$\frac{\sqrt{6}}{3}$.
在Rt△AOH中,sin∠AHO=$\frac{AO}{AH}$=$\frac{\sqrt{3}}{2}$.
∴∠AHO=60°.
即二面角A-PD-B的大小为60°.
点评 此题主要考查异面直线的角度、二面角的平面角的计算,考查线面垂直,考查学生分析解决问题的能力,属于中档题.

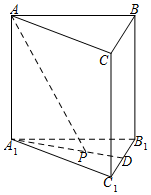 已知正三棱柱(底面是正三角形,且侧棱与底面垂直的棱柱)ABC-A1B1C1体积为$\frac{9}{4}$,底面边长为$\sqrt{3}$.若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为( )
已知正三棱柱(底面是正三角形,且侧棱与底面垂直的棱柱)ABC-A1B1C1体积为$\frac{9}{4}$,底面边长为$\sqrt{3}$.若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为( )| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
| A. | 1 | B. | 2 | C. | -1 | D. | $\sqrt{2}$ |
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | -1 |
| A. | $\frac{y^2}{25}+\frac{x^2}{16}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | C. | $\frac{x^2}{25}+\frac{y^2}{9}=1$ | D. | $\frac{x^2}{16}+\frac{y^2}{9}=1$ |
| A. | a>b>c | B. | c>a>b | C. | b>a>c | D. | c>b>a |
| A. | [1,2] | B. | [$\frac{1}{2}$,2] | C. | [$\frac{1}{2}$,1] | D. | (-∞,1) |
| A. | 0 | B. | 1 | C. | 2 | D. | 0或2 |
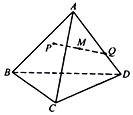 如图,在三棱锥A-BCD中,AB⊥AD,AC⊥AD,∠BAC=60°,AB=AC=AD=4,点P,Q分别在侧面ABC棱AD上运动,PQ=2,M为线段PQ中点,当P,Q运动时,点M的轨迹把三棱锥A-BCD分成上、下两部分的体积之比等于$\frac{π}{{48\sqrt{3}-π}}$.
如图,在三棱锥A-BCD中,AB⊥AD,AC⊥AD,∠BAC=60°,AB=AC=AD=4,点P,Q分别在侧面ABC棱AD上运动,PQ=2,M为线段PQ中点,当P,Q运动时,点M的轨迹把三棱锥A-BCD分成上、下两部分的体积之比等于$\frac{π}{{48\sqrt{3}-π}}$.