题目内容
12.函数f(x)的定义域为R+,且对于任何正实数x、y都有f(xy)=f(x)+f(y),若f(8)=6,则f($\sqrt{2}$)=( )| A. | 1 | B. | 2 | C. | -1 | D. | $\sqrt{2}$ |
分析 利用赋值法,有f(8)=f(4)+f(2),f(2)=f(2)+f(2),f(2)=f($\sqrt{2}$)+f($\sqrt{2}$),可求得f($\sqrt{2}$)
解答 解:∵对于任何正实数x、y都有f(xy)=f(x)+f(y),∴f(8)=f(4)+f(2),f(4)=f(2)+f(2),∴f(2)=2,
∵f(2)=f($\sqrt{2}$)+f($\sqrt{2}$),∴f($\sqrt{2}$)=1
故选:A.
点评 本题考查了抽象函数的赋值法,属于基础题.

练习册系列答案
相关题目
3.运行下面的程序中,若输入x的值为5,则输出的y的值为( )


| A. | 16 | B. | 17 | C. | 18 | D. | 19 |
7.周长为9,圆心角为1rad的扇形面积为( )
| A. | $\frac{9}{2}$ | B. | $\frac{9}{4}$ | C. | π | D. | 2 |
17.在等差数列{an}中,an>0,且a1+a2+…+a10=30,则a5+a6的值( )
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
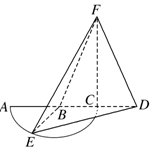 如图,以AC=2为直径的⊙B,点E为$\widehat{AC}$的中点,点D在直径AC延长线上,CD=1,FC⊥平面BED,FC=2.
如图,以AC=2为直径的⊙B,点E为$\widehat{AC}$的中点,点D在直径AC延长线上,CD=1,FC⊥平面BED,FC=2.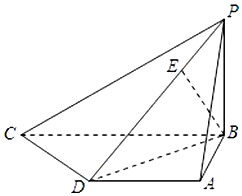 已知四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,AB=AD=1,BC=2,又PB⊥平面ABCD,且PB=1,点E在棱PD上,且BE⊥PD.
已知四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,AB=AD=1,BC=2,又PB⊥平面ABCD,且PB=1,点E在棱PD上,且BE⊥PD.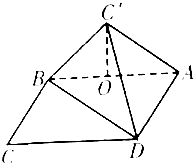 如图.在矩形ABCD中.AB=3 $\sqrt{3}$,BC=3,沿对角线BD把△BCD折起.使C移到C′.且C′在面ABC内的射影O恰好落在AB上.
如图.在矩形ABCD中.AB=3 $\sqrt{3}$,BC=3,沿对角线BD把△BCD折起.使C移到C′.且C′在面ABC内的射影O恰好落在AB上.