题目内容

13．若定义域为R的函数f（x）满足：对任意两个不相等的实数x1，x2，都有$\frac{{{x_2}f（{x_1}）-{x_1}f（{x_2}）}}{{{x_1}-{x_2}}}＜0$，记：a=4f（0.25），b=0.5f（2），c=0.2f（5），则（　　）
A．a＞b＞cB．c＞a＞bC．b＞a＞cD．c＞b＞a

分析 ∴对任意两个不等的正实数x1，x2，都有$\frac{{x}_{1}{x}_{2}（\frac{1}{{x}_{1}}f（{x}_{1}）-\frac{1}{{x}_{2}}f（{x}_{2}））}{{x}_{1}-{x}_{2}}＜0$⇒$\frac{\frac{1}{{x}_{1}}f（{x}_{1}）-\frac{1}{{x}_{2}}f（{x}_{2}）}{{x}_{1}-{x}_{2}}＜0$，令g（x）=$\frac{1}{x}f（x）$，易得g（x）在（0，+∞）上递减即可．

解答 解：定义域为R的函数f（x）满足：对任意两个不等的实数x1，x2，都有$\frac{{{x_2}f（{x_1}）-{x_1}f（{x_2}）}}{{{x_1}-{x_2}}}＜0$，
∴对任意两个不等的正实数x1，x2，都有$\frac{{x}_{1}{x}_{2}（\frac{1}{{x}_{1}}f（{x}_{1}）-\frac{1}{{x}_{2}}f（{x}_{2}））}{{x}_{1}-{x}_{2}}＜0$⇒$\frac{\frac{1}{{x}_{1}}f（{x}_{1}）-\frac{1}{{x}_{2}}f（{x}_{2}）}{{x}_{1}-{x}_{2}}＜0$，
令g（x）=$\frac{1}{x}f（x）$，易得g（x）在（0，+∞）上递减，a=4f（0.25）=g（0.25），b=0.5f（2）=g（2），c=0.2f（5）=g（5），
∴g（0.25）＞g（2）＞g（5），⇒a＞b＞c．故选：A．

点评 本题考查了构造新函数，函数的单调性的运用，属于基础题．

练习册系列答案
相关题目
3．运行下面的程序中，若输入x的值为5，则输出的y的值为（　　）
A．16B．17C．18D．19
4．下列四个命题中：
①“等边三角形的三个内角均为60°”的逆命题；
②“若k＞0，则方程x2+2x-k=0有实根”的逆否命题；
③“全等三角形的面积相等”的否命题；
④“若ab≠0，则a≠0”的否命题．
其中真命题的序号是（　　）
A．②、③B．③、④C．①、④D．①、②
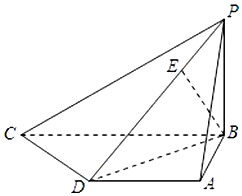1．已知四棱锥P-ABCD中，底面ABCD是直角梯形，AD∥BC，AB⊥BC，AB=AD=1，BC=2，又PB⊥平面ABCD，且PB=1，点E在棱PD上，且BE⊥PD．
（Ⅰ）求异面直线PA与CD所成的角的大小；
（Ⅱ）求证：BE⊥平面PCD；
（Ⅲ）求二面角A-PD-B的大小．
8．已知两点A（-1，2），B（m，3）．且实数m∈[-$\frac{\sqrt{3}}{3}$-1，$\sqrt{3}$-1]，求直线AB的倾斜角α的取值范围．
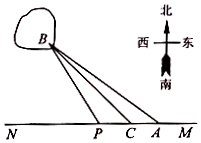18．如图，已知A，B两镇分别位于东西湖岸MN的A处和湖中小岛的B处，点C在A的正西方向1km处，tan∠BAN=$\frac{3}{4}$，∠BCN=$\frac{π}{4}$，现计划铺设一条电缆联通A，B两镇，有两种铺设方案：①沿线段AB在水下铺设；②在湖岸MN上选一点P，先沿线段AP在地下铺设，再沿线段PB在水下铺设，预算地下、水下的电缆铺设费用分别为2万元∕km、4万元∕km．
（1）求A，B两镇间的距离；
（2）应该如何铺设，使总铺设费用最低？
5．在平面直角坐标系xOy中，F是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的左焦点，点P在椭圆上，直线PF与以OF为直径的圆相交于点M（异于点F），若点M为PF的中点，且直线PF的斜率为$\sqrt{3}$，则椭圆的离心率为$\sqrt{3}$-1．
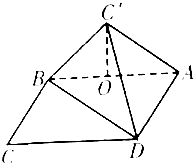15．如图．在矩形ABCD中．AB=3 $\sqrt{3}$，BC=3，沿对角线BD把△BCD折起．使C移到C′．且C′在面ABC内的射影O恰好落在AB上．
（1）求证：AD⊥BC′；
（2）求证：平面DBC′⊥平面ADC′；
（3）求三棱锥C′-ABD的体积．
16．直线l过抛物线C：y2=4x的焦点F交抛物线C于A、B两点，则$\frac{1}{{|{AF}|}}+\frac{1}{{|{BF}|}}$的取值范围为（　　）
A．{1}B．（0，1]C．[1，+∞）D．$[{\frac{1}{2}，1}]$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网